São dados, graficamente, o eixo maior e os focos de uma elipse. Descreva um método da construção de pontos da elipse com régua e compasso, baseado apenas na Definição 22-1.

Temos os seguintes elementos:

onde o segmento representa o eixo maior e , representam os focos da elipse.

Note que podemos desenhar uma circunferência de centro e raio e uma outra circunferência de centro e raio . Essas circunferências irão se encontrar em dois pontos, como mostra a figura a seguir.

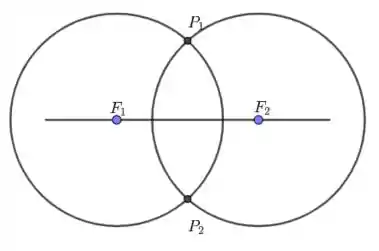
Note que e , de modo que , o que demonstra que está sobre a elipse. Se continuarmos fazendo isso, obteremos vários pontos da elipse, o que nos permitirá traçá-la.