Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 17.Exercício - Ex. 28
Calcule a área das bases de um prisma triangular reto cujas faces laterais estão contidas nos planos:
Passo 1
A ideia aqui é a seguinte, nós vamos desenhar esses três planos:
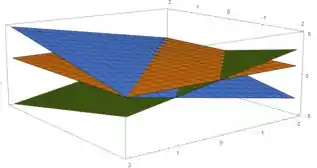
Percebe que dá pra encaixar um prisma aí entre esse planos? A gente quer calcular a área da base do prisma triangular reto que cabe ali.
O primeiro passo pra isso é encontrar as retas onde esses planos se intersectam, porque elas vão das as arestas do prisma:
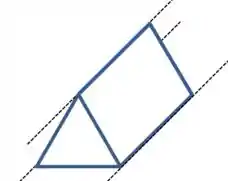
Ok, então vamos procurar essas arestas.
Passo 2
Pra encontrar a interseção dos planos e , temos que resolver esse sistema:
Pela primeira equação temos:
Substituindo isso na segunda:
Ou seja, nossa reta pode ser parametrizada da seguinte forma:
Para a interseção entre e o sistema é:
Fazendo quase a mesma coisa de antes:
Então a parametrização é:
E a interseção entre e tem esse sistema aqui:
Subtraindo as duas equações, descobrimos que:
E substituindo isso em uma das outras equações:
Então a parametrização é:
Ok, já temos as três retas.
Passo 3
Então ficamos com essas retas aqui:
Beleza, e nosso problema é: qual a área da base do prisma triangular reto que tem essas retas como arestas?
Bom, pra saber quais são os pontos dessas retas que vão formar nosso prisma, temos que encontrar o plano que seja perpendicular às três, e ver onde as retas cruzam esse plano.
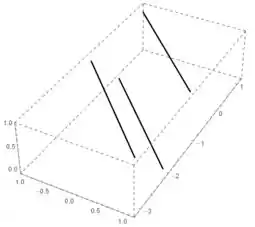
Para um plano ser perpendicular a uma reta, ele precisa ter seu vetor normal paralelo ao vetor diretor da reta.
Se um plano tem vetor normal , então a equação geral é:
Como todas as nossas retas tem vetor diretor , a equação do nosso plano é:
E a constante só muda a “posição inicial” do plano, então podemos escolher sem problemas:
Passo 4
Ok, próximo passo é: achar os pontos em que as nossas retas cruzam o plano.
A primeira reta tem:
Substituindo isso na equação do nosso plano:
A segunda reta tem:
Substituindo isso na equação do nosso plano:
E a terceira reta:
Substituindo isso na equação do nosso plano:
Passo 5
Então, se as nossas equações de retas são:
Substituindo , e :
Agora é só descobrir a área do triângulo (base do prisma) formado por esses três pontos , e .
Daí vamos usar essa fórmula aqui:
Começamos calculando esse produto vetorial:
Tirando a norma desse vetor:
Então a área que estamos procurando é:
Resolvido!
Resposta
A área das bases do prisma triangular é .