Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 15.Exercício - Ex. 14
Em relação a um sistema ortogonal de coordenadas, sejam
Mostre que existe um único ponto comum a essas três retas e calcule o volume do tetraedro determinado por elas e pelo plano .
Passo 1
Para começarmos a resolução, vamos considerar as nossas retas e .
Primeiramente, desenvolveremos cada uma das equações da reta, a fim de acharmos o ponto de interseção entre as três retas.
Passo 2
Começando pela reta , temos:
Para a reta , temos:
E para a reta , temos:
Dessa forma, podemos notar que as retas três retas podem ser igualadas, pois satisfazem mutuamente a condição de , porém, obrigatoriamente com .
Passo 3
Agora, vamos resolver o sisteminha para acharmos os valores pedidos:
É importante notarmos que, realmente com , o sistema de equações tem como solução os valores que nós achamos para e .
Logo, o ponto de interseção de tais retas é .
Passo 4
Por fim, para calcularmos o volume do tetraedro, vamos analisar a figura ilustrativa da nossa situação:
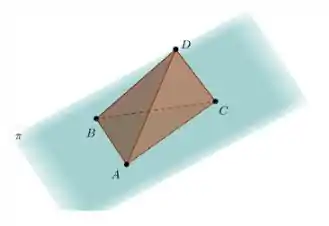
Basta agora, acharmos as coordenadas dos pontos e , achando a interseção das retas com o plano. Com tais coordenadas em mãos, é fácil acharmos a área da base e altura do nosso tetraedro.
Passo 5
Temos, então:
Começando pela área da base, vamos aplicar o produtor vetorial com dois lados da base:
Para a altura do tetraedro, temos:
Passo 6
Como temos a área da base e altura, usando a fórmula do volume de um tetraedro conseguimos calcular facilmente o volume pedido:
Resposta
O ponto comum é e o volume,