∑ 1 = O 1 , e 1 → , e 2 → , e 3 → e ∑ 2 = O 2 , f 1 → , f 2 → , f 3 → são dois sistemas de coordenadas tais que O 2 = 1,1 , 1 ∑ 1 e a matriz de mudança de base E = e 1 → , e 2 → , e 3 → para a base F = ( f 1 → , f 2 → , f 3 → ) é: ( a ) Obtenha, em relação ao sistema ∑ 1 , equações vetoriais dos eixos coordenados O 2 u ,O 2 v e O 2 w , e equações gerais dos planos coordenados O 2 u v , O 2 u w e O 2 v w do sistema ∑ 2 ( b ) Supondo que ∑ 1 seja ortogonal, obtenha em relação a ∑ 2 , equações gerais dos planos bissetores dos diedros determinados pelos planos coordenados O 1 x y ,O 1 x z e O 1 y z

a )O 2 u = 1,1 , 1 + λ [ 1,1 , 0 ] O 2 v = 1,1 , 1 + λ [ 0,1 , 0 ] O 2 u = 1,1 , 1 + λ [ 0,1 , 1 ] O 2 u v → z - 1 = 0 O 2 u w → 1 + y - x - z = 0 O 2 v w → x - 1 = 0 b )2 u + v + 2 + w = 0 ; v + w = 0 u + v = 0 ;v + u + w + 1 = 0 w + u + 2 = 0 ; w - u = 0

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 21.Exercício - Ex. 4

e são dois sistemas de coordenadas tais que e a matriz de mudança de base para a base é:

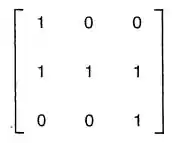
Obtenha, em relação ao sistema , equações vetoriais dos eixos coordenados e , e equações gerais dos planos coordenados e do sistema

Supondo que seja ortogonal, obtenha em relação a , equações gerais dos planos bissetores dos diedros determinados pelos planos coordenados e

Passo 1

Vamos no passo a passo, indicando o ponto como as antigas coordenadas (antes da transformação) e como as novas (após a transformação). O objetivo é correlacionar e com e . Seguindo a mesa ideia discutida na página nós temos que as coordenadas se correlacionam com as novas da seguinte forma:

Onde são as coordenadas de e é o coeficiente da matriz de transformação (na linha e na coluna) de base de uma base para a outra, ou de e para f ou de .

Logo:

Isolando os termos e nós teremos:

Passo 2

E aí podemos escrever a coordenada da seguinte forma:

Onde podemos ver a matriz de transformação como:

Então , e

Logo a equação dos eixos ordenados e (começando em ) serão:

E uma forma fácil de entender a equação dos planos é so você ver qual a regra de um plano convencional? Basta fazer . Logo a equação da origem em e plano é fazer , logo:

Passo 3

A equação dos planos bissetores usualmente é dada pelas seis equações:

Só que como essas estão em função de e nós teremos:

Logo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove as partes (a) e (c) do Teorema 3.2.3

O que pode ser dito sobre dois vetores não nulos u → e v → que satisfazem a equação u + v = u + | v | ?

Prove as partes (d) e (e) do Teorema 3.2.3

Sejam p 0 = ( x 0 ,y 0 ,z 0 ) e p = ( x ,y ,z ) . Descreva o conjunto de todos os pontos ( x ,y ,z ) para os quais ‖ p - p 0 ‖ = 1 .

Verifique a validade da desigualdade de Cauchy-Schwarz. (a) u = 4 ,1 ,1 ,v = ( 1 ,2 ,3 ) (b) u = 1 ,2 ,1 ,2 ,3 ,v = ( 0 ,1 ,1 ,5 , - 2 ) (c) u = 1 ,3 ,5 ,2 ,0 ,1 ,v = ( 0 ,2 ,4 ,1 ,3 ,5 )