Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 82
Quais são os pontos da hipérbole em que a reta normal contém
o centro?
um foco?
Passo 1
Pois bem, diferentemente do que acontece com a elipse para os tipos que hipérbole que podem ser ilustras com os exemplos a seguir
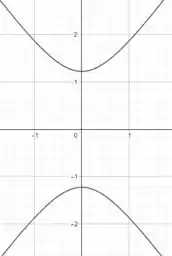
Podemos perceber que para a reta normal que é uma reta perpendicular a algum plano ou ponto em específico para o caso da hipérbole vamos ter que para que essa reta passe pelo centro ou pelo foco, os pontos aos quais nossa reta será dotada devem ser apenas os vértices da mesma tendo em vista que o centro e os focos são colineares.
Resposta
Em ambos os casos, os pontos vão ser somente os vértices.
Exercícios de Livros Relacionados
Obtenha, em cada caso, uma equação reduzida da hipérbole:Os vértices são 2,0 e - 2,0 e os focos, 3,0 e - 3,0 .Os vértices são - 15 , 0 e 15 , 0 e as assíntotas tem equações 5 y - 4 x = 0 e 5 y + 4 x =
Prove que o produto das distâncias de um ponto da hipérbole às assíntotas é a b c 2 .
Obtenha, em cada caso, uma equação reduzida da hipérbole:Os vértices são 2,0 e - 2,0 e os focos, 3,0 e - 3,0 .Os vértices são - 15,0 e 15,0 e as assíntotas tem equações 5 y - 4 x = 0 e 5 y + 4 x = 0 .
A hipérbole H tem centro O, focos em um dos eixos coordenados, e contém os pontos A e B. Escreva equações reduzidas de H e de suas assíntotas e determine os focos e vértices. A = 6 , 7 , B = - 1,0 . A
Obtenha, em cada caso, uma equação reduzida da hipérbole:Os vértices são 2,0 e - 2,0 e os focos, 3,0 e - 3,0 .Os vértices são - 15,0 e 15,0 e as assíntotas tem equações 5 y - 4 x = 0 e 5 y + 4 x = 0 .