Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 18.Exercício - Ex. 9

O segmento é a base de um triângulo isósceles de vértice e é também a interseção desse triângulo com o retângulo de vértices , , e . Os cinco pontos são coplanares. Conhecendo , e , obtenha as coordenadas de e .

Passo 1

Em um problema desse tipo, o primeiro passo é visualizar a figura:

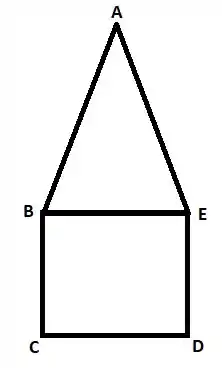
Como primeiro passo, vamos calcular alguns lados da figura. Primeiro o lado :

Assim, os lados e do triângulo medem . Já para o lado :

Portantoos lados e do retângulo medem .

Uma observação importante: eu supus que e fossem vértices consecutivos do retângulo, mas o enunciado não explicita isso necessariamente. Poderiamos também supor que fosse a diagonal do retângulo. Todavia, é usual usarmos a ordem alfabética para distribuir os pontos numa figura geométrica, então vamos seguir essa ideia...

Passo 2

Todos os pontos estão num mesmo plano, assim como os vetores e . Vamos achar o vetor normal a esse plano:

Por simplicidade, vamos usar

Todos os vetores do plano deve ser normais a ele!

Vamos procurar primeiro . Para isso, montamos o vetor:

Assim, como esse vetor deve ser ortogonal a :

Assim,

Além disso, temos que . Assim, como , temos que

Logo,

Assim,

Passo 3

Sabemos também que a distância de até deve ser :

Logo,

Portanto,

Logo,

Obtemos dois pontos:

Nesses caso,

Note que o primeiro ponto coincide com , então não é uma resposta válida. Isso ocorre pois pertence ao mesmo plano, à mesma reta e tem a mesma distância de que . Desta forma, a resposta válida é