Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 4
a) Seja a altura do triângulo relativa ao lado . Prove que
b) Escreva expressões análogas à do item (a) para as outras duas alturas.
c) Sejam , e pontos quaisquer tais que . Baseando-se no item (a), obtenha uma fórmula para calcular a distância de à reta determinada por e .
Passo 1
Bom, para resolver esse problema, vamos montar o triângulo e o paralelogramo gerado por e :
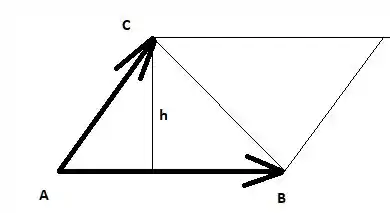
A altura do paralelogramo é a mesma altura do triângulo . Sabemos que a área do paralelogramo é dada pela norma do produto vetorial:
Sabemos também que
Nesse caso, a base é . Assim,
Portanto,
Passo 2
Para as demais alturas, a lógica será a mesma:
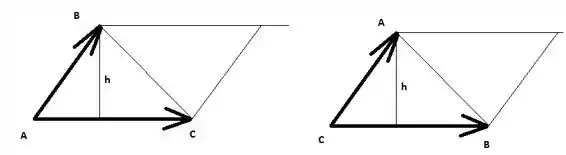
No primeiro caso,
No segundo,
Passo 3
No item (c), queremos a distância do ponto até a reta . Mas note que essa distância é dada exatamente pela altura calculada no item (a):
Resposta
Demonstração.