Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.1 - Ex. 1d
Seja V o conjunto de todos os pares ordenados de números reais e considere as operações de adição e multiplicação por escalar definidas em e por e
- Mostre que valem os Axiomas , e .
Passo 1
Vamos lá, são 3 axiomas então essa questão vai ser mais curtinha, mas não vamos desanimar, vamos começar.
Axioma 7: Produto da soma
Axioma 8: Soma do produto
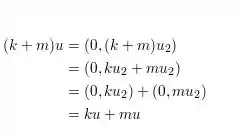
Axioma 9: Produto do produto
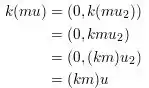
Devemos tomar cuidado com os axiomas por conta da necessidade de termos uma regra especial no nosso produto, mas fora isso é só seguir as regras convencionais.
E esses são os axiomas do produto, finalmente terminamos! \o/
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Seja V o conjunto de todos os pares ordenados de números reais e considere as operações de adição e multiplicação por escalar definidas em u=( u 1 ,u 2 ) ev =( v 1 ,v 2 ) por u +v =u 1 +v 1 ,u 2 +v 2
Seja V o conjunto de todos os pares ordenados de números reais e considere as operações de adição e multiplicação por escalar definidas em u=( u 1 ,u 2 ) ev =( v 1 ,v 2 ) por u +v =u 1 +v 1 + 1 ,u 2 +
Determine se o conjunto equipado com as operações dadas é um espaço vetorial. Para os que não são espaços vetoriais, identifique os axiomas que falham.O conjunto de todos os pares de números reais da
Seja V o conjunto de todos os pares ordenados de números reais e considere as operações de adição e multiplicação por escalar definidas em u=( u 1 ,u 2 ) ev =( v 1 ,v 2 ) por u +v =u 1 +v 1 ,u 2 +v 2
Determine se o conjunto equipado com as operações dadas é um espaço vetorial. Para os que não são espaços vetoriais, identifique os axiomas que falham.O conjunto de todos os pares de números reais da