Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 26
Seja o triângulo de vértices , e . Determinar o ângulo interno ao vértice . Qual o ângulo externo ao vértice ?
Passo 1
Então galera, antes de tudo vamos esboçar um triângulo qualquer com vértices , e aqui, se liga:
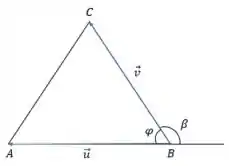
Por que nosso esboço está dessa forma? Vamos lá! O enunciado quer que encontremos o ângulo interno e o ângulo externo ao vértice , certo? Sendo assim, chamamos de o ângulo interno e de o ângulo externo. Show! Além disso, em azul desenhamos dois vetores formados a partir do triângulo que ajudarão demais na nossa resolução! Os vetores são:
e
Ou melhor:
Vamos guardar todas essas informações, belê? Show!
Passo 2
De acordo com o que estudamos no capítulo em questão do Winterle, temos que o produto escalar entre dois vetores é dado da seguinte forma:
No qual é o ângulo entre os dois vetores. No nosso caso temos que o ângulo é , então:
Isolando o ângulo:
Encontrando o módulo dos vetores:
Para o segundo vetor:
Passo 3
Substituindo as informações que encontramos na equação que escrevemos, teremos:
E de acordo com o que estudamos em Trigonometria, qual é o ângulo cujo cosseno resulta em ? Espero que tenha acertado; o ângulo é . Logo:
E esse é o ângulo interno que queríamos encontrar, galera! Ademais, agora que encontramos o ângulo interno, qual seria o ângulo externo? Por geometria, temos que:
Logo:
E estão aí nossos ângulos, pessoal! 😉
Resposta
e