Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 1- Ed: 6º - Capítulo 6.4 - Ex. 20

Seja V um espaço vetorial euclidiano . Se u   ϵ   V ,   W = [ u ] e E é a transformação linear que associa a cada vetor de V sua projeção ortogonal sobre W, mostre que:

v - E ( v ) ≤ v - w ,   ∀   v   ϵ   V   e   ∀   w   ϵ   W

Passo 1

Como W = [ u ] e u   ϵ   V , quer dizer que W tem só uma dimensão e no espaço, que se resume a uma reta, e v   é um vetor solto no espaço, desse jeito:

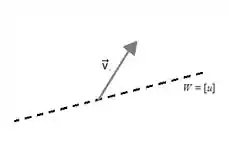
O enunciado diz que E ( v )   é a projeção de v em W = [ u ] , logo:

E ( v ) = P w v

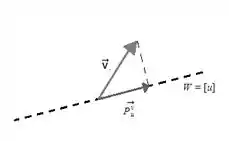
Lembrando da relação v = P w v + P w T v ou v -   P w v = P w T v

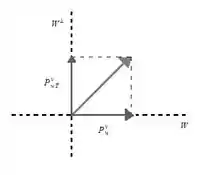
Podemos perceber que :

P w T v ≤ v

Passo 2

Agora o vetor w que pertence a W = [ u ] , vamos estudar o vetor v - w :

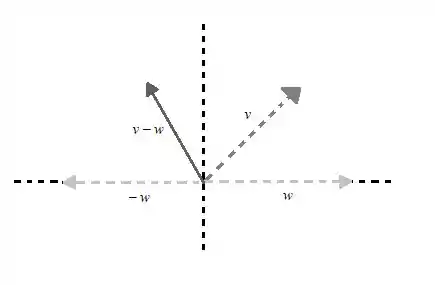
Podemos observar que v ≤ v - w

Passo 3

Dessa forma temos duas inequações:

P w T v ≤ v

v ≤ v - w

Unindo as duas equações temos:

P w T v ≤ v ≤ v - w

P w T v ≤ v - w

Sabemos que v -   P w v = P w T v e E ( v ) = P w v logo:

P w T v ≤ v - w

v - E ( v ) ≤ v - w ,   ∀   v   ϵ   V   e   ∀   w   ϵ   W

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se I B A = 0 1 0 1 1 0 1 1 1 determinar v A , sabendo que: v B = 3 - 2 0
Encontrar três matrizes semelhante à matriz: 1 1 - 1 2
Sabendo que: I B A = - 7 6 - 11 8e A = 1 ,3 ,2 ,- 4 , determine a base B .
Em relação aos operadores dados, determinar a matriz de T na base A e, a seguir, utilizar a relação entre matrizes semelhantes para calcular a matriz de T na base B . T :R 3 → R 3 ,T x , y , z = ( x -
Seja T :R 2 → R 2 um operador linear. Consideremos as bases A canônica e B = { 4 ,1 ,- 11 , - 3 } . Sabendo que T B = 3 5 1 2 determinar T A , utilizando a relação entre matrizes semelhantes.