Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 35.Problemas - Ex. 7
Seja m uma matriz 3X3 escalonada. Prove que o det[m] é o produto dos elementos da diagonal principal. Conclua que se det[m]=0 então a última linha de m é nula. Deduza daí que se uma matriz 3 x 3 tem determinante nulo, alguma de suas linhas é combinação linear das outras duas.( Perceba que isto da outra demonstração para propriedade 7)
Passo 1
Fala galerinha , vamos resolver mais uma questão do nosso livro de Geometria analítica e Álgebra Linear !!!
Primeiramente vamos escrever nossa matriz m e encontrar o determinante.
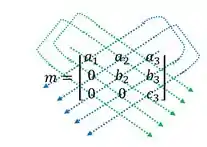
Mostrando que o determinante é o produto dos elementos da diagonal da matriz.
Com isso em mente, vamos então ao próximo passo...
Passo 2
Este passo será encontrar a situação para qual o valor do
E para isto possa ocorra, um de seus elementos devem ser igual a zero.
E como forma de demonstração é proposto que suas linhas são Linearmente independentes,
Resolvendo o sistema no próximo passo, ....
Passo 3
Agora vamos resolver,
Sendo,
Na próxima equação,
Para finalizar, a última equação ,
Resposta
Então, podemos concluir que a matriz
det[
E como é L.I a última linha é nula,
E seus coeficientes,
Espero que ajudem nos estudos, até próxima