Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 5.7 - Ex. 6
Seja o operador linear que transforma em e em , conforme figura.
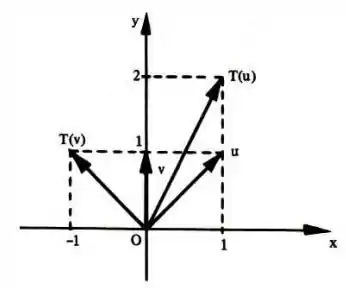
a) Dar a lei do operador .
b) Determinar a transformação linear que transforma em e em .
Passo 1
O problema fornece uma transformação linear por meio de uma figura. Dela, conseguimos tirar que
Precisamos dar a lei do operador, isto é, escrever e no item (b) achar sua inversa.
Para isso, vamos escrever primeiro:
Mas como , temos que
Assim, como temos e , podemos construir a matriz canônica para a transformação:
Passo 2
Desta forma, podemos escrever uma expressão para a transformação fazendo o produto de matrizes:
Logo,
Passo 3
Note que
Logo, é invertível. Para achar sua inversa, vamos usar o truque que só vale para matrizes :
Assim,
Assim, a transformação inversa é dada por
Logo,
Resposta
Exercícios de Livros Relacionados
Mostrar que se A e B são matrizes ortogonais, então A B também será ortogonal.
Mostrar, por meio da multiplicação de matrizes, que uma rotação de 30 ° seguida de uma rotação de 60 ° resulta em uma rotação de 90 ° .
Verificar quais das seguintes matrizes são ortogonais e, dentre estas, determinar as que representam rotações: 1 3 2 3 2 3 2 3 - 2 3 1 3 2 3 1 3 - 2 3
Determinar a e b para que os seguintes operadores no R 3 sejam simétricos: T :R 3 → R 3 ,T x ,y ,z = 3 x - 2 y ,a x + y - 3 z ,b y + z T :R 3 → R 3 ,T x ,y ,z = x + 2 z ,a x + 4 y + b z ,2 x - 3 y + z
Determinar a projeção ortogonal do vetor ( 1,1 , 0 , - 1 ) ∈R 4 sobre o subespaço W = x , y , z , t ∈R 4x - y - z = 0ez - 2 t = 0 }