Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.2 - Ex. 8b
Seja um subespaço de .
b) Determine uma base para .
Passo 1
Vamos continuar a questão então! Na última alternativa encontramos os geradores de , no entanto, é necessário que eles sejam linearmente independentes para serem uma base, vamos checar isso, beleza?
Passo 2
Checar isso no entanto, vai dar um trabalhinho, é preciso encontrar uma solução tal que:
só tenha a solução trivial . ou seja:
De forma, que é conveniente escalonarmos a seguinte matriz, de forma a simplificar o nosso problema:
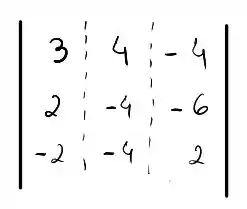
Bora lá!
Passo 3
Primeiro, vamos identificar como o primeiro elemento da primeira coluna, o pivô, dividindo a primeira linha por 3, saca só:
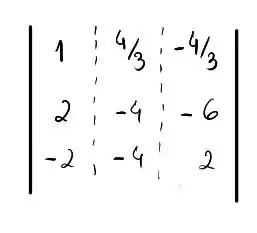
Agora, precisamos eliminar os dois elementos restantes na primeira coluna. Nós podemos subtrair da segunda linha a primeira linha multiplicada por 2, e somar a terceira linha a primeira linha multiplicada por 2, de forma que:
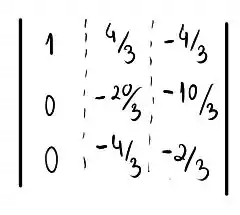
Agora, precisamos deixar o segundo termo da diagonal como 1, isso é possível se multiplicarmos à segunda linha por , obtendo:
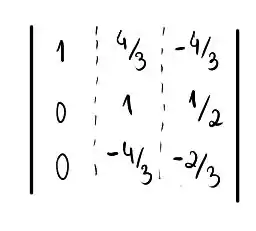
Ainda precisamos eliminar o termo que falta abaixo da diagonal na terceira linha, para isso vamos somar a segunda linha multiplicada por na terceira linha para obter:
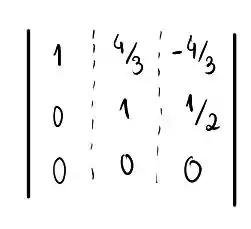
Note que a última linha desapareceu completamente, portanto, um dos nossos vetores é linearmente dependente dos outros dois! Sendo assim, vamos tentar obter uma relação para obter o vetor dependente, em termos dos outros dois, saca só!
Passo 4
Nos restou o seguinte sistema de equações:
e
Como temos 3 parâmetros para duas equações, vamos escolher um deles livremente, no caso , de forma que:
Nossa equação original tem então a forma:
Se escolhermos , obtemos
Ou seja, qualquer par construído com os 3 vetores acima pode ser a base escrevendo o terceiro em termos dos vetores de base, já que eles são linearmente independentes 2 a 2. A questão foi isso, te vejo na próxima!