Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 19
Seja a quádrica de equação
- Faça uma translação do sistema de coordenadas para eliminar os termos de primeiro grau e identifique a quádrica.
- Obtenha, em relação ao sistema antigo, uma equação do plano que contém a “cintura” de .
- Faça um esboço de e desenhe, em vista frontal, suas projeções ortogonais sobre os planos , e .
Passo 1
Então, como temos uma equação do segundo grau a três incógnitas com termos lineares e sem termos mistos, podemos fazer uma translação para eliminar estes termos lineares.
Este é o nosso objetivo. Eliminar estes termos lineares para poder identificar a nossa quádrica. Então, temos que fatorar a equação. Portanto,
Vamos fazer uma translação da origem para . Para isto, temos o seguinte sistema:
E assim teremos a seguinte equação:
O que consiste em um hiperboloide de uma folha!
Passo 2
A “cintura” dita no enunciado da questão consiste na menor elipse possível, sendo esta obtida pela interseção do hiperboloide com algum plano.
Para o hiperboloide obtido na questão, a menor elipse será dada por
Quando fizermos a interseção com o plano . E ela será a menor possível quando , o que nos dá a seguinte elipse (no novo sistema):
Portanto, o plano, no sistema antigo, é .
Passo 3
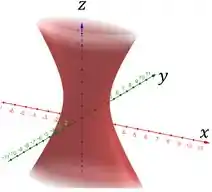
O esboço das quádricas é algo um pouco mais difícil. Aqui, iremos mostrar como ela está se comportando no geral.
O importante, é sempre colocarem o vértice dela e indicar os eixos, como ela se comporta (eixo de simetria e etc). Portanto, temos o seguinte paraboloide:
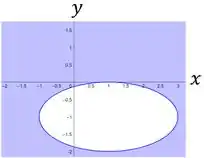
Agora, vamos fazer as projeções do paraboloide com os planos , e . Começando por , temos:
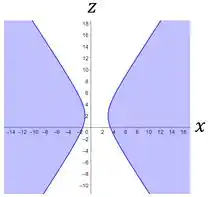
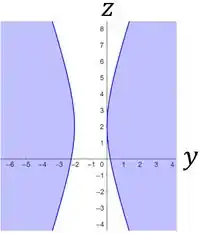
Em relação a , temos:
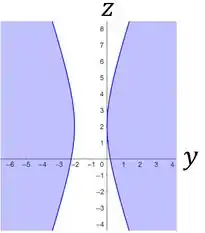
Por fim, em relação ao plano , temos:
Resposta
- A translação foi:
- O esboço do hiperboloide é:
E com isto obtemos o hiperboloide de uma folha .
Já a projeção nos planos , e , são, respetivamente:
