Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.2 - Ex. 31a
Seja a reta num sistema de coordenadas de . Descreva o subespaço .
Passo 1
O espaço subespaço será perpendicular ao espaço da reta . Então, vamos visualizar a reta
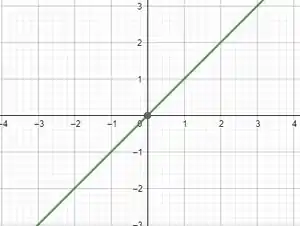
Passo 2
Vamos agora visualizar a reta
Passo 3
Se sobrepormos uma reta a outra, veremos que o espaço da reta
Resposta
O subespaço é composto pela reta
Exercícios de Livros Relacionados
Existe algum produto interno euclidiano ponderado em R 3 no qual os vetores ( 1,2 ) e ( 3 , - 1 ) formem um conjunto ortonormal? Justifique sua resposta.
Suponha que R 3 tenha o produto interno euclidiano. Encontre dois vetores de comprimento 1 que sejam ortogonais a cada um dos três vetores u 1 = 1,1 , - 1 ,u 2 = - 2 , - 1,2 e u 3 = - 1,0 , 1 .
Suponha que M 22 tenha o produto interno U , V = t r U T V = t r V T U definido no Exemplo 6 da Seção 6.1. Descreva o complemento ortogonal do subespaço de Todas as matrizes diagonais.Todas as matrize
Seja W o plano y z num sistema de coordenadas x y z de R 3 . Descreva o subespaço W ⊥ .
Prove que a Fórmula (4) é válida com quaisquer vetores u → e v → num espaço com produto interno V .