Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 4.8 - Ex. 43

Seja a transformação linear:

S :   R 3 → R 4 ,     S x , y , z = ( x + y , z , x - y , y + z )

a) Calcular ( S ∘ T ) ( x , y ) se

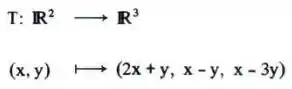
b) Determinar a matriz canônica de S ∘ T e mostrar que ela é o produto da matriz canônica de S pela matriz canônica de T .

Passo 1

A questão fornece duas transformações lineares S e T . No item (a) devemos achar a transformação composta:

S ∘ T x , y = S T x , y = S ( 2 x + y , x - y , x - 3 y )

Para ficar mais fácil a visualição, vou chamar a , b , c = ( 2 x + y , x - y , x - 3 y ) . Assim,

S ∘ T x , y = S a , b , c = ( a + b , c , a - b , b + c )

Notemos que

a + b = 2 x + y + x - y = 3 x

a - b = 2 x + y - x + y = x + 2 y

b + c = x - y + x - 3 y = 2 x - 4 y

Assim,

S ∘ T x , y = ( 3 x , x - 3 y , x + 2 y , 2 x - 4 y )

Passo 2

Agora no item (b) temos que achar as matrizes canônicas T , [ S ] , [ S ∘ T ] e verificar que

S ∘ T = S ⋅ [ T ]

Para a matriz [ T ] , temos que calcular T ( 1 ,   0 ) e T ( 0 ,   1 ) :

T 1 ,   0 = ( 2 ,   1 ,   1 )

T 0 ,   1 = ( 1 , - 1 , - 3 )

Assim,

T = 2 1 1 - 1 1 - 3

Já para [ S ] ,

S 1 ,   0 ,   0 = ( 1 ,   0 ,   1 ,   0 )

S 0 ,   1 ,   0 = ( 1 ,   0 , - 1 ,   1 )

S 0 ,   0 ,   1 = ( 0 ,   1 ,   0 ,   1 )

Portanto,

S = 1 0 1 0 0 1 1 0 - 1 1 0 1

Já para composta, usando a resposta do item (a):

S ∘ T 1 ,   0 = ( 3 ,   1 ,   1 ,   2 )

S ∘ T 0 ,   1 = ( 0 , - 3 ,   2 , - 4 )

Desta forma,

S ∘ T = 3 1 0 - 3 1 2 2 - 4

Para verificar a relação S ∘ T = S ⋅ [ T ] , vamos fazer o produto de matrizes:

1 0 1 0 0 1 1 0 - 1 1 0 1 ⋅ 2 1 1 - 1 1 - 3 = 2 + 1 1 1 - 1 - 3 2 - 1 1 + 1 1 + 1 - 1 - 3 = 3 1 0 - 3 1 2 2 - 4

Vemos que a relação é de fato verificada!

Resposta

S ∘ T x , y = ( 3 x , x - 3 y , x + 2 y , 2 x - 4 y )

T = 2 1 1 - 1 1 - 3

S = 1 0 1 0 0 1 1 0 - 1 1 0 1

S ∘ T = 3 1 0 - 3 1 2 2 - 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

21. Já que a base canônica de R n é tão simples, por que quereríamos representar um operador linear de R n em alguma outra base?
20. Se A e B forem matrizes semelhantes, digamos, B = P - 1 A P , então segue do Exercício 19 que A e B têm os mesmos autovalores. Suponha que λ seja um desses autovalores comuns e x seja um autovetor
17. Sejam C e D matrizes m × n e B = v 1 , v 2 , … , v n uma base de um espaço vetorial V . Mostre que se C x B = D x B , qualquer que seja x em V , então C = D .
15. Seja λ um autovalor de um operador linear T : T → V . Prove que os autovetores de T associados a λ são os vetores não nulos no núcleo de λ I - T .
14. Seja T : M 22 → M 22 definido por: T a b c d = 2 c a + c b - 2 c d (a) Encontre os autovalores de T .(b) Encontre bases dos autoespaços de T .