Exercícios de Matriz que Representa uma TL - Lista de Exercícios Resolvida

Consideremos a transformação linear definida por e as bases do e do . Determinar a matriz

Mostrar que a matriz do operador linear identidade

em uma base qualquer, é a matriz identidade .

Seja a transformação linear , e as bases e . Determinar . Qual a matriz , onde é a base canônica do ?

A matriz que representa a transformação linear definida por:

é:

Sejam e a transformação linear que é representada na base canônica de pela matriz:

Se é um autovetor de , então é igual a:

Escolha uma opção:

1. 7
2. 3
3. 2
4. 4
5. 1

Seja um operador linear cujo polinômio característico é:

Considere as seguintes afirmações

(I)

(2) é diagonalizável se, e somente se , existirem cinco vetores distintos linearmente independentes tais que , e

(3) Se é uma matriz cujo polinômio característico é igual ao polinômio característico de , então então existe uma base de tal que

Considere a função definida por:

(Observe que é a transformação que deriva o polinômio)

Escreva a matriz de na base canônica de .

À questão “Seja a transformação linear definida por e . Encontre a matriz de associada a base canônica de ”, Joãozinho respondeu:

Seja uma transformação linear e considere e bases de e , respectivamente. Qual é a definição do elemento linha e coluna da matriz , que representa nas bases e ?

Seja o espaço vetorial dos polinômios de grau . Seja dado por . Seja base de . Se é a matriz que representa a transformação linear escolhendo base do domínio e do contradomínio, então é:

Considere munido do produto interno usual e seja uma base de que satisfaz:

Seja o operador linear simétrico cuja matriz, em relação à base , é

Então, os produtos internos são iguais, respectivamente, a

Escolha uma opção:

1. -11, -1 e -2
2. -11, -2 e -1
3. -1, -11 e -2
4. -2, -1 e -11
5. -1, -2 e -11
6. -2, -11 e -1

Seja a transformação linear tal que:

Se é a matriz que representa com respeito à base canônica de , então a soma dos elementos na segunda coluna da matriz é igual a:

Escolha uma opção:

1. -1
2. 1
3. 0
4. 2
5. -2

Seja uma base de . A transformação linear está definida através de , . Indique a matriz que representa a inversa de na base .

Seja a transformação linear dada por:

E sejam e bases para e respectivamente.

Determine .

Sejam e as bases de dadas por , , e seja a transformação linear tal que .

Sendo a transformação linear , determine .

Considere a transformação linear dada pela fórmula

Determine , onde e são as bases canônicas de e , respectivamente.

Sejam e as bases de dadas por , , e seja a transformação linear tal que .

Dado , determine .

Julgue verdadeira ou falsa cada afirmação. Justifique.

Existe transformação linear que satisfaz , , .

Qualquer que seja a transformação linear , seu núcleo tem dimensão pelo menos 16.

Seja uma transformação linear tal que a sua matriz , com respeito a um certo par de bases e , vale . Então é um isomorfismo.

Seja uma transformação linear cuja imagem é o plano e o núcleo é a reta que passa pela origem na direção do vetor . Assinale a matriz que pode representar :

Sejam vetores em

a)Seja a matriz cujas linhas são os vetorese , ou seja,

Encontre a matriz escalonada reduzida de

b)Considere

(b.1) Mostre que é um subespaço vetorial de

(b.2) Determine uma base para

c)Seja a transformação linear (ou matricial) dada por

(c.1) Determine a que representa a transformação

(c.2) Determine o posto e a nulidade de

(c.3) Determine uma base do espaço coluna de

Seja o espaço vetorial das matrizes quadradas de duas linhas e duas colunas. Para denote sua transposta, ou seja, se , então

Considere a aplicação dada por

(b) Determine uma base de (núcleo de ).

(c) T é bijetora?

(d) Seja base de . Determine .

(e) Determine uma base de (imagem de ).

Seja a transformação linear dada por , e base de .

b)Construa .

Sejam e . Considere o conjunto .

(a) Mostre que é base do .

(b) Determine e .

(c) Determine para .

(d) A projeção (não necessariamente ortogonal) de um vetor w sobre um vetor v, na direção de um vetor u, é o vetor w’ que tem a direção de v e tal que w-w’ tem a direção de u, como a figura abaixo.

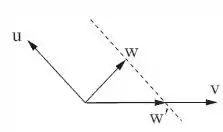
Encontre a matriz da transformação linear que é a projeção de (x,y) sobre na direção de .

Seja o espaço vetorial das matrizes quadradas de duas linhas e duas colunas.

Considere a aplicaçãodada por

d)Seja base de M2x2 e ϵ = {(1; 0), (0; 1)}

base de R². Determine

e)Encontre uma matriz A tal que , onde , como no item anterior

Sejam os vetores e Considere a transformação , dada por

(a) Calcule

(b) Mostre que é uma transformação linear.

(c) Determine uma base de

(d) Determine uma base de

(e) Determine a matriz canônica de , ou seja, a matriz e . (O mesmo que , ou ainda, )

Considere a transformação linear definida por:

(a) Determine a matriz da transformação linear T na base canônica.

(b) Determine a equação cartesiana da imagem de T. Lembre que:

(c) Considere a base:

Determine a matriz da transformação linear T na base .

(d) Considere o plano de equação cartesiana:

Determine uma base da imagem de pela transformação T.

Considere a matriz:

Determine a transformação associada à matriz com relação às bases , .

Seja a base canônica do e uma transformação linear tal que , e . A matriz de na base canônica é:

Seja linear e base de tal que , e . Qual é a representação matricial de utilizando a base no domínio e no contradomínio?

A matriz que representa a transformação linear definida por é

Sejam linear e a matriz que representa com relação à base canônica. Se , qual é a matriz de com relação à base ?

Sejam a base canônica de e . Considere a transformação linear tal que a matriz de com relação à base é dada por . Se , então é igual a:

Seja linear tal que e . A primeira coluna da matriz de com relação à base canônica é:

Seja uma transformação linear, , cuja imagem é a reta e o núcleo é o plano de equação . Assinale uma matriz que representa esta transformação linear: