Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 8.4 - Ex. 20
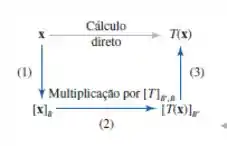
Seja uma transformação linear de um espaço vetorial de dimensão quatro com base num espaço vetorial de dimensão sete com base . Identifique os quatro espaços
vetoriais que contêm os vetores dos vértices do diagrama da figura.
Passo 1
Vamos lá! vamos fazer umas considerações pra resolver esse exercício.
Passo 2
Assim temos:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Para que valores de a , b e c (reais) as seguintes matrizes de M 2 R são semelhantes a - b b aec 0 0 - c
Seja V um espaço vetorial de dimensão finita. Sejam u e v dois vetores desse espaço com a seguinte propriedade: ∀ F ∈ V * F u = 0 ⟹ F v = 0 . Mostrar que u , v é LD.Sugestão: Se fossem LI, existiria u
Provar que todo sub-espaço vetorial W de V , com dim W = dim V - 1 , é o núcleo de uma forma linear não nula.
Provar que se A e B são semelhantes então A n e B n são semelhantes, para todo n ≥ 1 . Sendo p t um polinômio, p t = a 0 + a 1 t + … + a n t n , indicamos por p A a matriz p A = a 0 I + a 1 A + … + a
Sejam A, B, C, D matrizes de ordem n, sendo A e B semelhantes, C e D semelhantes. É verdade que A + C e B + D são semelhantes? E quanto a AC e BD?