Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 13.Exercício - Ex. 13
Sejam , , e .
a) Mostre que esses pontos são vértices de um quadrilátero plano.
b) Mostre que o quadrilátero do item (a) é convexo (um quadrilátero plano é convexo se nenhuma das retas que contêm seus lados separa os outros dois vértices, o que equivale a nenhum de seus vértices ser interior ao triângulo determinado pelos outros três).
c) Sabe-se da Geometria Plana que a reta que contém uma diagonal qualquer de um quadrilátero convexo separa os outros dois vértices. Utilize essa propriedade e do Exercício Resolvido 6-16 para descobrir quais são os lados e quais são as diagonais do quadrilátero do item (a).
Passo 1
Para provar que os pontos são vértices de um quadrilátero plano, basta mostrar que os vetores , e estão num mesmo plano. Para isso, basta mostrar que eles são LD.
As coordenadas desses vetores são
Assim,
Assim os vetores são LD e estão no mesmo plano. Provamos assim, que , , e são vértices de um quadrilátero plano.
Passo 2
No exercício 5-5 provamos que um ponto é interior ao triângulo de vértices , e se, e somente se, , com , e .
É isso que temos que fazer no item (b), provar que cada um dos vértices não é ponto interior do triângulo formado pelos outros três. Vamos fazer isso com ponto :
Escrevendo
Assim,
Da terceira equação tiramos que
Substituindo na primeira equação:
Note que como , não é ponto interior do triângulo . Isso acontece com todos os vértices desse quadrado, de modo que ele é convexo!
Passo 3
Agora vamos para o item (c). Note que
Fazendo um desenho:
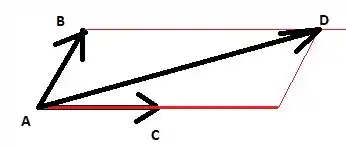
Ligando os pontos, obtemos o quadrilátero:
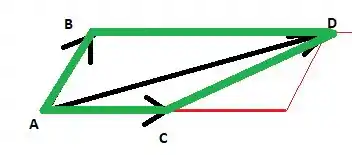
Os lados são: , , e . As diagonais: e .
Resposta
Demonstração.