Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 25.Problemas - Ex. 5

Sejam A = (0, 1, 0), B = (1, 0, 1), C = (1, 1, 0) e D = (0, 0, 1). Mostre que as retas AB e CD têm um ponto em comum, o qual pertence também à reta EF, onde E = (1, 0, 0) e F = (0, 1, 1). Interprete este resultado geometricamente.

Passo 1

Vamos encontrar os pontos que definem as paramétricas através das equações dadas no capítulo.

Dado dois pontos A = ( a ,   b ,   c ) e A ' = ( a ' ,   b ' ,   c ' ) , então

x = a + t a ' - a

y = b + t ( b ' - b )

z = c + t c ' - c

Vamos encontrar as equações paramétricas de cada reta:

Para a reta AB:

x = t ,   y = 1 ,   z = t ,         t   ∈   R

Para a reta CD:

x = 1 ,   y = 1 , z = t ,           t   ∈   R

Para a reta EF:

x = 1 ,   y = t , z = 1 ,           t   ∈   R

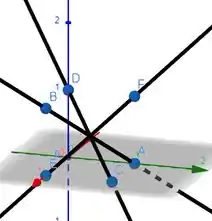
Se t for 1, as três retas se cruzam no ponto médio das retas, dessa forma, elas possuem o ponto (1/2,1/2,1/2) em comum.

Resposta

Demonstração

Exercícios de Livros Relacionados

Calcular o valor de m para que sejam concorrentes as seguintes retas:b) r 1 = x = m - t y = 1 + t z = 2 t e r 2 : x - 1 3 = y + 2 1 = z - 2
Dadas as retas r 1 = x - 1 2 = - y ; z = 3 e r 2 = x = t y = - 1 + t z = 2 + t Encontrar equações reduzidas na variável x da reta que passa por ( 0,1 , 0 ) e pelo ponto de interseção de r 1 com r 2 :
Determine na reta r = x = 2 + t y = t z = - 1 + 2 t Um ponto equidistante do ponto A=( 2 , - 1 , - 2 ) e B = ( 1,0 , - 1 ) .
Determine os pontos da reta r : x = 2 + t , y = 1 + 2 t ,z = 3 + 2 t que:Distam 6 unidades do ponto A = 2,1 , 3 ;
Determine os pontos da reta r : x = 2 + t , y = 1 + 2 t ,z = 3 + 2 t que:Distam 2 unidades do ponto B = 1 , - 1,3 ;