Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.5 - Ex. 13

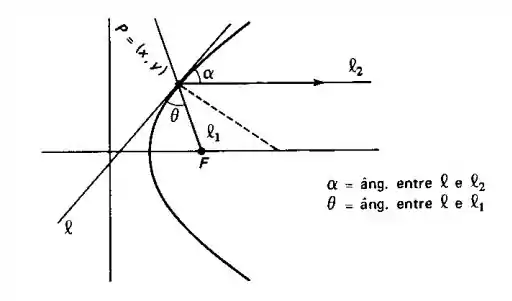
Sejam P um ponto de uma parábola e l a reta tangente à parábola em P . Sejam l 1 a reta ligando o foco a P e l 2 a reta que passa por P e é paralela ao eixo, então os ângulos θ e α a seguir são iguais.

Passo 1

Pra poder demonstrar essa propriedade, vamos usar a parábola “deitada” e com centro na origem, porque essa é a mais fácil de mexer hahahah Mas ó, não tem nenhum problema de invalidar a nossa demonstração por ser um caso específico, porque qualquer parábola pode ser deslocada pra essa posição. Então bora! A equação da nossa parábola é:

y 2 = 4 p x

E por isso, o foco é F = ( p ,   0 ) . Vamos pegar um ponto qualquer P = ( x 0 ,   y 0 ) na parábola. O nosso objetivo é mostrar que o ângulo entre a reta l 1 e a reta n é igual ao ângulo entre a reta l 2 e a reta n , porque, como n é a reta normal, os ângulos α e θ que a gente quer são os complementares, e aí também vão ser iguais.

Passo 2

Vamos ver a inclinação da reta tangente t , derivando implicitamente a equação da parábola no ponto P :

y 2 = 4 p x

Derivando,

2 y 0 y ' = 4 p

y ' = 2 p y 0

Então, a inclinação da reta normal é:

y n ' = - y 0 2 p

Por fim, a inclinação de l 1 é:

m l 1 = y 0 x 0 - p

Passo 3

Então vamos calcular a tangente dos ângulos 90 ° - α e 90 ° - β :

t g ( 90 ° - α ) = - y 0 2 p - y 0 x 0 - p 1 - y 0 2 2 p x 0 - p

Desenvolvendo:

t g ( 90 ° - α ) = - x 0 y 0 + p y 0 - 2 p y 0 2 p x 0 - 2 p 2 - y 0 2

E aí, vamos usar a equação da parábola pra substituir o y 0 2 por 4 p x 0 !

t g ( 90 ° - α ) = - x 0 y 0 - p y 0 2 p x 0 - 2 p 2 - 4 p x 0 = - x 0 y 0 - p y 0 - 2 p x 0 - 2 p 2

Botando em evidência:

t g ( 90 ° - α ) = - y 0 x 0 + p - 2 p x 0 + p

Cortando o que tem pra cortar:

t g ( 90 ° - α ) = y 0 2 p

E agora vamos calcular a tangente de ( 90 ° - β ) , sabendo que a inclinação de l 2 é 0 .

t g ( 90 ° - β ) = 0 - y 0 2 p 1 - 0 y 0 2 p = y 0 2 p

Por isso,

t g 90 ° - α = t g 90 ° - β

t g α = t g β

E aí,

α = β

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

São dados, em cada caso, o parâmetro geométrico a e os focos de uma hipérbole. Obtenha uma equação algébrica de segundo grau em x e y que todo ponto x , y da hipérbole deve satisfazer. a = 3F 1 = 3 ,-
Calcule, em cada caso, a excentricidade da hipérbole H . 4 x 2 - y 2 = 16 . x 2 - 2 y 2 + 8 = 0 . O triângulo F 1 B 2 F 2 é retângulo. As diagonais do retângulo fundamental formam ângulos de 60 ° . Os
A figura 22-7 mostra um mapa onde figuram quatro estações transmissoras em terra, A ,B ,C e D . As estações B e C emitem simultaneamente sinais que são recebidos por um navio situado em P , e o sinal
Utilize seu programa gráfico para desenhar, no computador, hipérboles com excentricidades variando no intervalo ] 1 ,+ ∞ [ . Desenhe algumas com focos em O x , outras com focos em O y , use o mesmo va
Sejam k um número real, r uma reta e F um ponto, tais que m = d F , r0 . Prove quese 0k1 , todo ponto Q tal que d Q , F = k ⋅ d Q , r pertence à elipse de excentricidade k que tem F por foco e r por d