Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 122

Sejam k um número real, r uma reta e F um ponto, tais que m = d F , r > 0 . Prove que

  1. se 0 < k < 1 , todo ponto Q tal que d Q , F = k ⋅ d Q , r pertence à elipse de excentricidade k que tem F por foco e r por diretriz associada a ele.
  2. Se k > 1 , todo ponto Q tal que d Q ,   F = k ⋅ d Q , r pertence à hipérbole de excentricidade k que tem F por foco e r por diretriz associada a ele.

Passo 1

  1. Tomemos s como sendo uma reta que contém F e é perpendicular a r . Consideremos o número

    2. d = m k 2 1 - k 2

    Tal número é candidato ao “ c ”, que é motivado pela resposta do exercício 22-120 (a).

    Considere que O seja o ponto s que dista d de F e m + d de r . Veja a figura abaixo

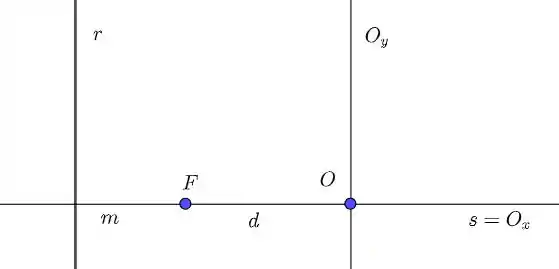
    Passo 2

    Na figura, temos

    O = 0 ,   0 ;         F = - d ,   0 ;             r : x = - m + d Considere Q = x ,   y um ponto genérico tal que

    d Q ,   F = k ⋅ d Q ,   r

    Passo 3

    Cálculo de d Q , F :

    d Q , F = x + d 2 + y 2

    Cálculo de d Q , r :

    d Q , r = x + m + d

    Passo 4

    Portanto, temos que

    x + d 2 + y 2 = k x + m + d ⟺

    x + d 2 + y 2 = k x + m + m k 2 1 - k 2 ⟺

    x + d 2 + y 2 = k x + m 1 - k 2

    Elevando ao quadrado,

    x + m k 2 1 - k 2 2 + y 2 = k 2 x 2 + 2 m x 1 - k 2 + m 2 1 - k 2 2 ⟺

    x 2 + 2 m x k 2 1 - k 2 + m 2 k 4 1 - k 2 2 + y 2 = k 2 x 2 + 2 m x k 2 1 - k 2 + m 2 k 2 1 - k 2 2 ⟺

    x 2 1 - k 2 + y 2 = m 2 k 2 1 - k 2 2 1 - k 2 ⟺

    x 2 1 - k 2 + y 2 = m 2 k 2 1 - k 2 ⟺ x 2 m 2 k 2 1 - k 2 2 + y 2 m 2 k 2 1 - k 2 = 1

    Note que temos uma elipse com a = m 2 k 2 1 - k 2 2 e b 2 = m 2 k 2 1 - k 2 . Note que

    c 2 = a 2 - b 2 = m 2 k 2 1 - k 2 2 - m 2 k 2 1 - k 2 = m 2 k 4 1 - k 2 2 ⟹ c = m k 2 1 - k 2 = d

    Passo 4

    Assim, vemos que F realmente é o foco da hipérbole, com k = e , que é exatamente o que queríamos mostrar.

    Passo 5

  2. Procedemos de maneira muito semelhante à letra (a). Comece tomando

d = m k 2 k 2 - 1

(que será candidato a c pelo exercício 22-120 (b)). Fazendo exatamente as mesmas contas, chegaremos em

x 2 m 2 k 2 k 2 + 1 2 - y 2 m 2 k 2 k 2 - 1 = 1

de modo que

c 2 = m 2 k 2 k 2 - 1 2 + m 2 k 2 k 2 - 1 = m 2 k 4 k 2 - 1 2 ⟹ c = m k 2 k 2 - 1 = d

de modo que mostramos que F é o foco.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo de uma hipérbole mede 6 e seus focos, situados sobre o eixo OY, são F'=( 0 ,- 4 )eF=( 0 ,4 ) . Qual é a equação dessa hipérbole?
Dados um ponto F, uma reta ∆ que não contém F e um número positivo e, seja X o conjunto dos pontos P do plano tais que d P , F d ( P , ∆ ) = e Prove:a) Se e1 então X é uma hipérbole.
Mostre que x =a cos ⁡ t , y =sin ⁡ t cos ⁡ t equações paramétricas de uma hipérbole. Qual é o domínio da variável t e quais são os focos dessa hipérbole?
Lembrando que m 2 -n 2 =m+n m–n , mostre que x–x 2 - a 2 = a 2 x +x 2 - a 2 e use este fato para concluir que, atribuindo a x valores muito grandes em módulo, o ponto ( x , b a x ) na assíntota da hip
Quais são as coordenadas dos focos da hipérbole x y=1 ?