Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 42

Utilize seu programa gráfico para desenhar, no computador, hipérboles com excentricidades variando no intervalo ] 1 ,   + ∞ [ . Desenhe algumas com focos em O x , outras com focos em O y , use o mesmo valor para a em todas, para facilitar a comparação.

Passo 1

O software que utilizaremos é o Geogebra. Você pode utilizá-lo acessando o link

https://www.geogebra.org/classic?lang=pt

Passo 2

Nos prints abaixo temos as hipérboles

x 2 a 2 - y 2 a 2 e 2 - 1 = 1

(com os focos no eixo O x ) e

y 2 a 2 - x 2 a 2 e 2 - 1 = 1

(com os focos no eixo O y ).

Vamos fixar a = 1.4 .

Passo 3

e = 1.2

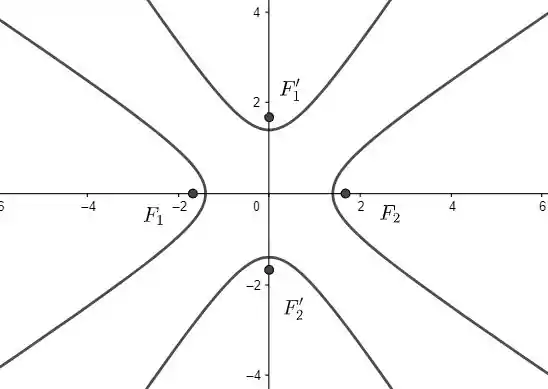
e = 2.2 . Note a rápida mudança no “achatamento” das hipérboles

e = 3

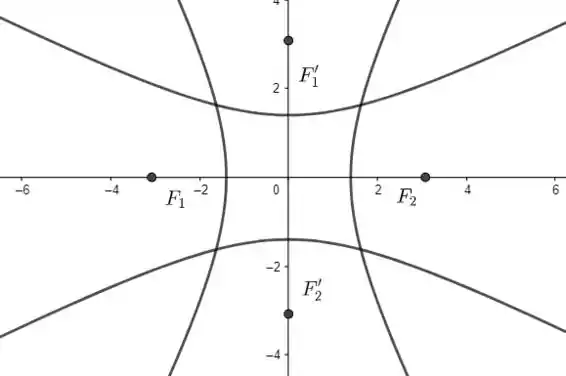
Note que conforme e vai aumentando, o foco vai se afastando cada vez mais da origem. Isso ocorre pois e = c / a e a é fixo. Logo, quando e aumenta, c tem que aumentar.

e = 20

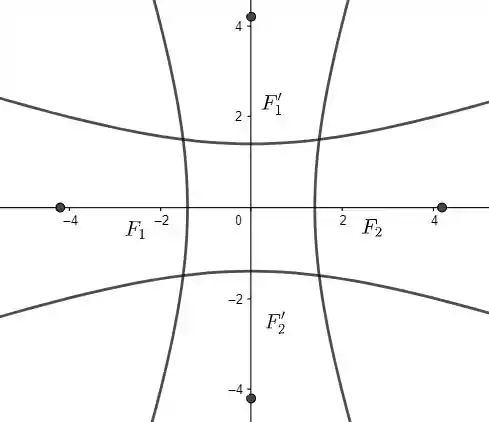
Veja que para um valor tão grande de e , as hipérboles se aproximam de retas paralelas ao eixo. Isso é esperado, já que o denominador de y 2 a 2 e 2 - 1 fica tão grande que podemos desprezar tal termo, ficando apenas com x 2 a 2 = 1 ⟹ x = ± a , que são as duas retas verticais representadas na figura. As retas horizontais são as retas y = ± a .

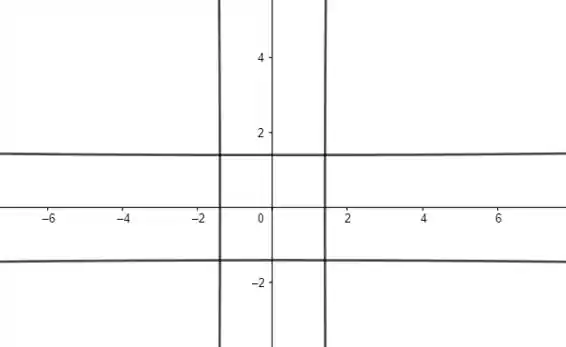
Passo 4

Conclusão: fixado a , ao aumentar e as hipérboles irão se aproximando de retas paralelas a um dos eixos ordenados.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Segundo a Geometria Elementar, se D é um ponto do lado BC do triângulo ABC então a reta AD é bissetriz do ângulo BÂC se, e somente se, A B ∙ C D = A C ∙ B D . Use este fato para mostrar que a tangente
Mostre que a equação da hipérbole com focos nos pontos F 1 = ( x 0 - c , y 0 ) e F 2 = ( x 0 + c , y 0 ) e satisfaz d i s t P , F 1 - d i s t P , F 2 = 2 a em que ac é x - x 0 2 a 2 - y - y 0 2 b 2 =
Identificar a cônica, achar a equação no último sistema de coordenadas utilizando e fazer um esboço do gráfico. x 2 - y 2 + 2 3 x y + 6 x = 0
Dados os dois focos de uma hipérbole e a distância entre os vértices, achar a equação da mesma.
Cada uma das equações a seguir representa o conjunto vazio, um ponto, uma reta, um par de retas paralelas, uma cônica ou um par de retas que se cortam na origem. Decida cada situações e determine as r