Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 25.Problemas - Ex. 3
Sejam AB e CD retas sem pontos em comum. Prove que elas são reversas se, e somente se, AC ∩ BD = ∅ e AD ∩ BC = ∅.
Passo 1
Se as retas AD e BC não se intersectam, assim como as retas AD e BC, então as retas AB e CD estão em planos diferentes, isto é, são reversas. Perceba o desenho. Caso se intersectassem, estariam no mesmo plano.
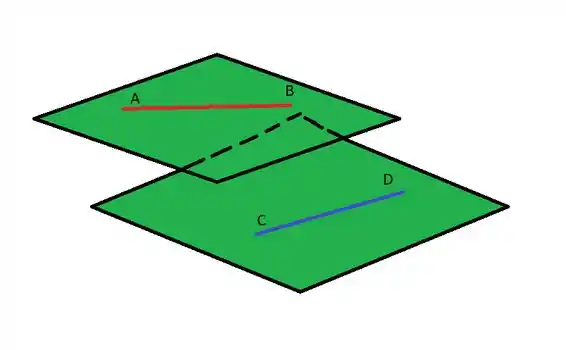
Resposta
Demonstração
Exercícios de Livros Relacionados
Seja o triângulo de vértices A 1 ,0 , - 2 ,B ( 2 , - 1 , - 6 ) e C ( - 4 ,5 ,2 ) .Estabelecer as equações paramétricas da reta suporte da mediana do triângulo A B C relativa ao lado B C .
Dados os pontos P 1 ( 7 , - 1 ,3 ) e P 2 ( 3 ,0 , - 12 ) , determinar:o ponto Q, que divide o segmento P 1 P 2 ao meio.
Dados os pontos P 1 ( 7 , - 1 ,3 ) e P 2 ( 3 ,0 , - 12 ) , determinar:o ponto P, que divide o segmento P 1 P 2 na razão 2 3 ;
Sejam as retas r : x = 2 + 3 t y = 4 + 5 t z = m te s : y = 2 x + 1 z = x 2 - 3 2 a) calcular o valor de m para que r e s sejam concorrentes;b) determinar, para o valor de m , o ponto de interseção de
25. Dadas as retas: r : y - 3 2 = z + 1 - 2 ; x = 2 e s :y = 2 x z = x - 3 e h :x = 3 + t y = 1 - 3 t z = t .Determina:O ponto de interseção de s e h;O ângulo entre r e s.