Suponha que um vetor do plano tenha um comprimento de unidades e aponte na direção que faz um ângulo de no sentido anti-horário a partir do eixo positivo e que um vetor daquele plano tenha um comprimento de unidades e aponte na direção e sentido do eixo positivo. O que pode ser dito sobre o valor de ?
Passo 1
Vamos ilustrar o enunciado a fim de facilitar o entendimento:
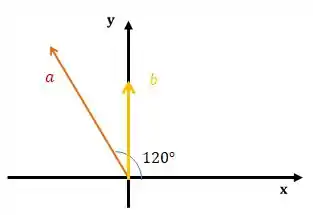
Pelos dados do enunciado temos que:
Assim,
Resposta
Logo,