Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 47b
(b) Se um tetraedro tem dois pares de arestas opostas ortogonais, as duas retas restantes são ortogonais.
Passo 1
Bora lá!
Para resolvermos esse exercício, vamos desenhar o nosso tetraedro ABCD, cujas faces BAC e CAD possuem ângulo reto em, respectivamente, e :
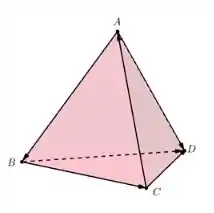
Passo 2
Primeiramente, utilizaremos a Relação de Euclides da letra (a) no nosso tetraedro e vamos levar em consideração que, devido ao ângulo reto, e . Dessa forma, temos
Passo 3
Logo, já que o produto escalar vetorial nula indica um ângulo reto, podemos concluir que o outro par de arestas, no caso e , também são ortogonais. 😉
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Seja o cubo de aresta a representado na Figura 2.17 . Determinar: E G → ⋅ C G →
Seja o cubo de aresta a representado na Figura 2.17 . Determinar: E D → ⋅ A B → O G →
Calcular os ângulos diretores do vetor v → = 6 , - 2,3 .
Determinar um vetor unitário ortogonal ao eixo O z e que forme 60 ° com o vetor i → .
O vetor v → é ortogonal aos vetores u → = 1,2 , 0 e w → = 2,0 , 1 e forma ângulo agudo com o vetor j → . Determinar v → , sabendo que v → = 21 .