Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 41

A B C é um triângulo, e P e Q são pontos tais que 3   A P → = A C → e 3   B Q → = 2   B C → . Calcule a razão entre as áreas dos triângulos B P Q e A B C .

Passo 1

Primeiro vamos desenha o triângulo A B C :

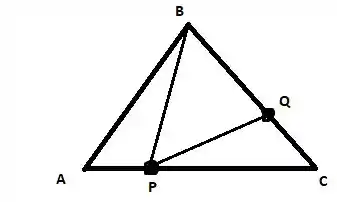
A área do triângulo A B C é dada por

A A B C = 1 2 B A → ∧ B C →

Já a área do triângulo B P Q é

A B P Q = 1 2   B P → ∧ B Q →

Assim, a razão entre as áreas é

r = A B P Q A A B C = B P → ∧ B Q → B A → ∧ B C →

Passo 2

Vamos escrever   B P → e   B Q → em termos de   B A → e  B C → :

B P → = B A → + A P → = B A → + 1 3   A C → = B A → + 1 3   - B A → + B C → = 2 3   B A → + 1 3   B C →

Analogamente,

B Q → = 2 3   B C →

Assim,

B P → ∧ B Q → = 2 3   B A → + 1 3   B C → ∧ 2 3   B C → = 4 9   B A → ∧ B C →

Passo 3

Portanto,

r = B P → ∧ B Q → B A → ∧ B C → = 4 9   B A → ∧ B C → B A → ∧ B C →

Tirando o 4 / 9 para fora:

r = 4 9 ⋅ B A → ∧ B C → B A → ∧ B C → = 4 9

Resposta

4 9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma chave de boca com 30c m de comprimento posicionada ao longo do eixo y aperta um parafuso colocado na origem. Uma força é aplicada no final do cabo da chave com direção dada por ( 0,3 , - 4 ) . Det
Demonstre a parte 6 do Teorema 8, ou seja, a × b × c = a ∙ c b - a ∙ b c
Suponha que a ≠ 0 .Se a ∙ b = a ∙ c é verdade que b = c ?Se a × b = a × c é verdade que b = c ?Se a ∙ b = a ∙ c e a × b = a × c é verdade que b = c ?
Seja P um ponto não pertenente ao plano que passa pelos pontos Q , R e S . Mostre que a distancia d do ponto P ao plano é d = a × b ∙ c a × b Onde a = Q R → , b = Q S → e c = Q P → .Utilize a fórmula
Seja v = 5 j e seja u um vetor com comprimento 3 com início na origem e que gira no plano x y . Determine o máximo e o mínimo valor possível para u × v . Qual a direção e o sentido de u × v ?