Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 2.Exercício - Ex. 1
- Vale a igualdade para quaisquer vetores e ? Justifique sua resposta. E quanto a ?
Passo 1
Inicialmente, desenharemos vetores quaisquer e veremos se a proposição serve para esses vetores! Se der certo, podemos afirmar que sim, se der errado, deu ruim!!
E após isso, faremos igualmente para a segunda proposição .
Passo 2
Começaremos com . O que ele diz é que o módulo da soma é a soma dos módulos. Será que isso é verdade?? Vamos começar!
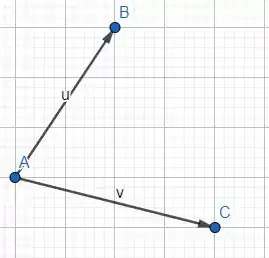
A soma de é representada no desenho como .
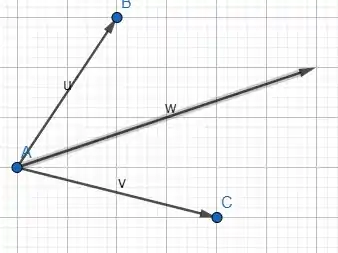
Vamos fechar esse triangulo.
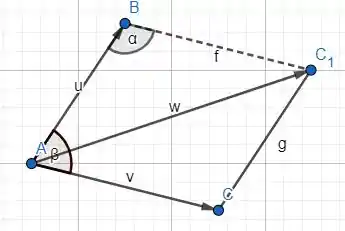
E temos um paralelogramo! Até porque o nome da regra é regra do parelelogramo, então temos coisas legais já que isso é um paralelogramo:
E que o segmento vale o módulo de , assim como mede o módulo de e mede o módulo de .
Resumindo, temos:
De posse disso tudo, eu vou fazer a lei dos cosenos nesse triângulo e ver se vai bater com aquilo que esperávamos.
Substituindo em função dos módulos, temos:
Ficou bem diferente né e pela fórmula que calculamos, vai depender do ângulo entre os vetores! O que o enunciado disse só vai ocorrer para !
Para , .
Então,
Viuu! Não é para todos os vetores, somente para um conjunto especial deles, aqueles que estão numa reta!!
Passo 3
Para provarmos a letra b) é bem mais fácil, substituiremos por . E vamos alterar a fórmula:
Sabendo que :
E da mesma forma que explicado para a soma, no caso da diferença aquilo dito no enunciado, não é verdade sempre mas sim um caso especial da difenreça de vetores. Ocorre quando .
Para , .
Então:
É apenas um caso especial da diferença de vetores.
Resposta
Ambas são falsa, pois não ocorrem sempre, mas sim só quando o ângulo entre os vetores é de (para a soma) e quando o ângulo entres os vetores é de (para a diferença).