Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.Exercícios Suplementares - Ex. 3
Com quais valores de s é o espaço solução de
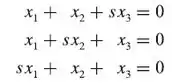
uma reta pela origem, um plano pela origem, a origem ou todo o ?
Passo 1
Vamos lá! Antes de tudo precisamos escrever a matriz canônica da nossa transformação:
Calculando , temos:
Se fizermos , encontramos , .
Se fizermos que é considerada uma solução trivial para o sistema, .
Agora vamos substituir pelos valores encontrados para cada situação.
Passo 2
Vamos lá! Precisamos escrever nosso sistema de equações em forma de matriz, assim temos:
Se fizermos temos:
Assim temos que: .
Como para temos essa transformação é aceitando somente a solução trivial.
Sendo , nosso sistema tem como resposta , que é a origem do nosso .
Passo 3
Vamos lá! Precisamos escrever nosso sistema de equações em forma de matriz, assim temos:
Se fizermos temos:
Assim temos que: .
Sendo , nosso sistema tem como resposta , que é um plano que passa pela origem do sistema.
Lembrando a nossa Equação do plano sendo , como nosso plano passa pela origem.
Passo 4
Vamos lá! Precisamos escrever nosso sistema de equações em forma de matriz, assim temos:
Se fizermos temos:
Assim temos que: .
Sendo , nosso sistema tem como resposta uma reta, já que todos valores precisam ser iguais.
Imagine a equação do plano sendo
Substituindo pelos valores que encontramos:
Como é uma constante, nossa equação representa uma reta.
Essa é a equação da reta que passa pela origem.
Resposta
Para , nosso sistema é a origem de .
Para , nosso sistema é um plano que passa pela origem.
Para , nosso sistema é uma reta que passa pela origem.