Verdadeiro ou falso? Justifique sua resposta.

a) é LD é LD.

b) é LI é LI.

c) Se e não são nulos, então é LD é LD.

d) é LI é LD.

e) Se é LD, então tanto pode ser LD como LI.

f) Se é LI, então tanto pode ser LD como LI.

Vamos analisar cada uma das afirmativas beleza?

a) Falso. Se é LD, quer dizer que são vetores coplanares, até aí beleza. Mas para que seja LD, eles precisam ser paralelos, e não necessariamente eles serão sabe? 3 vetores coplanares podem estar apontando cada um pra uma direção. Olha essa imagem pra entender melhor, os 3 vetores são LD pois são coplanares, mas se tirarmos um deles, teremos vetores LI pois não serão paralelos. (condição para que dois vetores sejam LD):

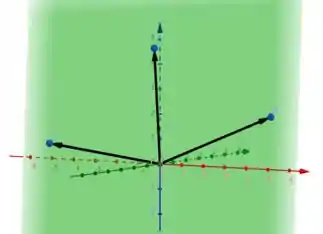
b) Falso. Não necessariamente. podem ser vetores não paralelos, mas se o vetor que surgir for coplanar com eles dois, os 3 formarão um conjunto LD, igual na imagem acima.

c) Falso. A justificativa é a mesma da letra a, não importa os coeficientes que estão multiplicando os vetores, pois eles ainda vão estar na mesma direção, mudando apenas módulo ou sentido.

d) Falso. Se é LI, são vetores não coplanares, beleza. Mas até aí, nada nos garante que serão dois vetores paralelos, podemos ter algo assim, onde temos 3 vetores LI, mas se tirarmos um deles, ainda teremos vetores LI.

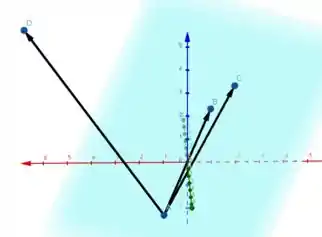
e) Verdadeiro. Em 3 vetores coplanares, podemos ter dois que são paralelos, ou podem não ser, assim como na primeira imagem desse exercício.

f) Verdadeiro. são vetores não paralelos, e o vetor que vai surgir pode ser coplanar a eles (igual na primeira imagem) ou não (igual na segunda imagem)