Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 20.Exercício - Ex. 14b

Verifique para quais pontos X da reta r a área do triângulo A B X é a menor possível e comente as peculiaridades geométricas de cada caso.

b) A = 1 ,   0 ,   3                           B = 2 ,   1 ,   2                           r : 2 x - y + z = 0 = x + z - 1

Passo 1

Da reta r , temos

2 x - y + z = 0 x + z - 1 = 0

Da segunda equação, temos z = - x + 1 , substituindo na primeira:

2 x - y - x + 1 = 0

y = x + 1

Então, nossa reta pode ser escrita assim:

x ,   y ,   z = ( x ,   x + 1 ,   - x + 1 )

Substituindo x pelo parâmetro t , um ponto genérico X da reta r é dado por

X = t ,   t + 1 ,   - t + 1

Sabendo que A B → = B - A = 1 ,   1 ,   - 1 e A X → = X - A = t - 1 ,   t + 1 ,   - t - 2 , a área do triângulo A B X é metade da área do paralelogramo, ou seja:

A t = A B → ∧ A X → 2

Substituindo os vetores que temos:

A t = 1 ,   1 ,   - 1 ∧ t - 1 ,   t + 1 ,   - t - 2 2

A t = ( - 1 ,   3 ,   2 ) 2

Calculando o módulo do vetor:

A t = 1 + 9 + 4 2

A t = 14 2

Passo 2

Cara, olha que coisa, chegamos que a área do nosso triângulo é

A t = 14 2

Não temos nenhuma variável dentro dessa expressão, o nosso t sumiu, ou seja, a área sempre vai ser 14 2 , independente do ponto X que tivermos.

Por que isso acontece? Olha só:

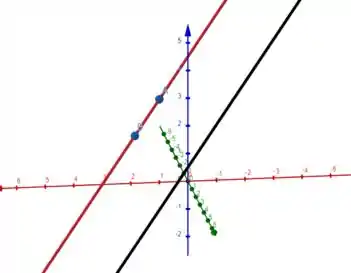
A reta formada pelo vetor diretor A B → é paralela à reta r , então, a área do triângulo A B X sempre vai ser a mesma ok?

Resposta

Para qualquer ponto X , pois A B → é paralelo à reta r .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva as equações das retas que contém as diagonais do paralelogramo de vértices A = 1 , - 2 , 2 ,B = ( 2,1 , - 1 ) , C = ( 1 , - 6 , 8 ) e D = 2 , - 3,5 .
Sejam A = 1,0 , 1 , B = 0,1 , 1 , C = ( 3 , - 2,1 ) e D = ( 0,0 , 1 ) . (a) Determine um ponto X na reta A B tal que a área do triângulo C D X seja 2. Quantos pontos X existem nessas condições?(b) Qua
(b) determine m e n para que o ponto P = 1 , m , n pertença à reta dada. Escreva equações da reta r que passa por A = ( 1 , - 2,3 ) e é paralela à reta x - 4 2 = y - 45 7 = z - 1 ;
Dados A = 1,2 , 4 , B = 2,4 , 1 , C = 1,1 , 5 e D = 2,2 , x , determine x para que os 4 pontos sejam coplanares
É dada a reta a x = 1 + 2 t y = - 3 - t z = 3 t . Determine os pontos da reta a cuja distância ao ponto X = ( - 6,2 , - 3 ) seja 3 3 .