Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 3f
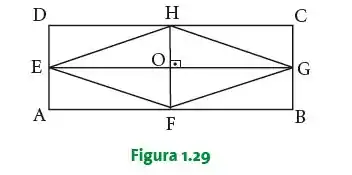
Com base na Figura , determinar os vetores a seguir, expressando-os com origem no ponto :
Passo 1
Vamos lá, vamos primeiro localizar os vetores e da figura, onde o vetor começa no ponto e termina no ponto e o vetor começa no ponto e termina no ponto :
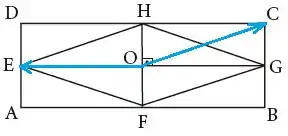
Agora vamos multiplicar por os dois vetores:
Como queremos expressar com origem no ponto devemos deslocar o vetor inicial para esse ponto:
Passo 2
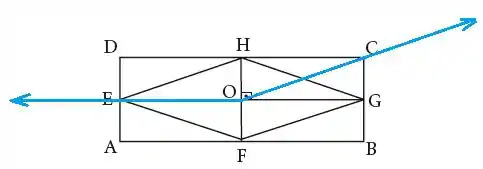
Para calcular a soma devemos colocar o ponto de término do vetor tocando o ponto de início do vetor , vamos então deslocar o vetor :
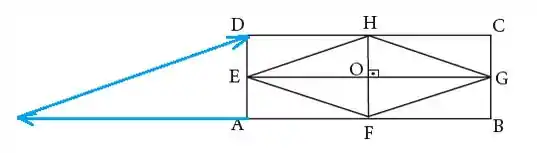
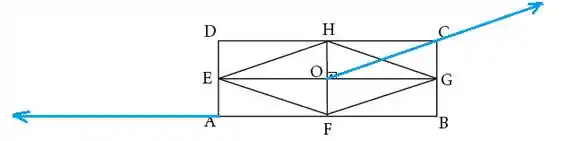
Agora a soma desses dois vetores é o resultado o ponto de início do primeiro vetor com o ponto de término do último vetor:
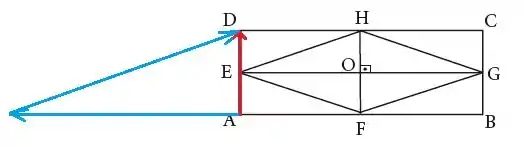
O que nos resulta no vetor:
Resposta
Exercícios de Livros Relacionados
Qual é o simétrico do vetor u = (2, 5) em relação à reta y= x 2
Se os segmentos orientados AA′ e BB′ são equipolentes, prove que também são equipolentes os segmentos orientados AB e A ′B ′
Se os pontos A e B são equidistantes da origem e os segmentos orientados OA e BC são equipolentes, prove que OC e AB são perpendiculares.
Seja AA′ uma diagonal de um cubo e sejam B, C e D os vértices desse cubo que estão mais próximos de A. Mostre que AA′ é perpendicular a BC e BD e conclua que AA′ é perpendicular ao plano BCD. Mostre a
Ache quatro pontos A, B, C e D no espaço, cujas coordenadas sejam 1 ou 0, de modo que ABCD seja um tetraedro regular. Verifique que duas arestas opostas desse tetraedro são ortogonais.