12. Calcule a soma dos seis vetores que têm por representantes segmentos orientados com origem em cada um dos vértices, e extremidade no centro de um mesmo hexágono regular.
Passo 1
Desenhando esse hexágono, temos:
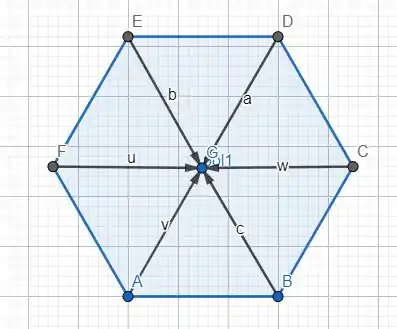
Passo 2
A soma que a gente quer é a seguinte:
Só que vamos lá. Quanto é a soma de ?
Ora, eles tem o mesmo módulo, mesma direção e sentidos contrários, logo a soma é zero!!
Então .
Da mesma forma que e .
Passo 3
Dando prosseguimento no passo 3, temos:
Então, a soma desses vetores é igual a .