Matriz Inversa
Produzido por Bruno PestanaTeoria
Introdução
Bom, até agora você deve ter estudado muitos tipos de matrizes e várias operações para fazer com elas, mas... já se perguntou como se inverte uma matriz? Bom, existem vários jeito de se inverter e vários truques também e é isso que vamos ver nesse capitulo.
Para começar, o que seria a matriz inversa??? Vamos pensar em um número real. Por exemplo, o . O inverso de , ou seja , ahhh então ???? Não!! O que acabei de escrever não existe! Então o que você pode dizer que tem de especial com um número e o seu inverso??
E aí pensou???
Um número multiplicado pelo seu inverso, sempre dá !
E é exatamente isso a propriedade mais importante das matrizes inversas! Você pode me dizer quem seria o das matrizes??? O que o tem de especial?? Ahh ele é o numero que faz com que qualquer número multiplicado por ele, dê o próprio número:
E quem faz isso no universo das matrizes??
A matriz identidade!!
Logo, a matriz inversa multiplicada pela matriz original dá , ou seja, a matriz identidade:
E qualquer matriz admite inversa??
NÃO!!! Só matrizes quadradas admitem inversa!!
Ah, então todas as matrizes quadradas têm inversa? Bom, mais ou menos. Lembra do escalonamento? Então, se você tem uma matriz quadrada e quer saber se ela é invertível é só você escalonar ela! Se alguma linha da matriz tiver só zeros, ela não é invertível. Caso contrário, ela é invertível! Lembrando que ela deve ser quadrada haha.
Outra maneira de sabermos se uma matriz é invertível é:
- Se o determinante for , a matriz não é invertível
- Se o determinante for diferente de , ela é invertível
Ótimo, sabemos quando uma matriz é invertível, mas como eu inverto?? Bom, vamos ver isso agora!
Invertendo matrizes
Você já sabe o que uma matriz inversa tem de tão especial, mas como achamos a matriz inversa??
Existem alguns jeitos. Vamos pegar por exemplo essa matriz aqui:
Já sabemos que ela é quadrada, então podemos invertê-la :D. Acho que o jeito mais intuitivo é pela definição. O jeito que vou mostrar pode ser aplicado para uma MATRIZ DE QUALQUER ORDEM! No caso, vamos fazer para ordem .
Vamos achar a inversa de:
Então:
Agora é só montar o sistema!
Assim, a nossa matriz inversa fica:
E pronto achamos a nossa matriz inversa! Mas é meio trabalhoso né? Por isso que vou ensinar um truque que SÓ VALE PARA MATRIZES :
Considerando a matriz original , podemos dizer que a matriz inversas também pode ser escrita como:
E é o que chamamos de determinante da matriz ! Vamos ver muita coisa sobre determinantes mais tarde no curso, mas já to dando um spoiler aqui haha. Vamos reescrever:
Vamos ver se esse truque da certo mesmo:
Igualzinho a solução do nosso sistema!
Po, mas meio complicado lembrar disso. Vou botar aqui um passo a passo pra você se acostumar:
Passo 1: Troque os elementos da diagonal principal.
Passo 2: Multiplique por os elementos da diagonal secundária.
Passo 3: Divida a matriz pelo determinante da matriz original.
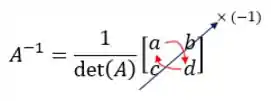
Invertendo matrizes e ordem maiores
Bom, agora que você já sabe inverter matrizes , vamos aprender um método bem prático que nem o das matrizes , só que agora vai servir pra matrizes de quaisquer ordens. Para isso é preciso que você esteja bem em escalonamento.
Vamos pegar essa matriz por exemplo:
Não da pra aplicar o método anterior que aprendemos para matrizes , mas poderíamos calcular pela definição, montando um sistema linear agora de equações que não é nem um pouco prático. Por isso vamos usar o método do escalonamento. Basta seguir os passos abaixo:
Passo 1: Pegue a matriz que você quer inverter e coloque ao lado da identidade
Passo 2: Escalone a primeira matriz até transformá-la na identidade, ou seja, escalone até a sua forma reduzida e, enquanto isso, aplique as mesmas operações na matriz identidade ao lado.
Passo 3: A matriz inversa é a matriz que se formou no lado direito do algoritmo.
Resumindo:
Passo 1: Pegue a matriz que você quer inverter e coloque ao lado da identidade
Passo 2: Escalone a primeira matriz até transformá-la na identidade, ou seja, escalone até a sua forma reduzida e, enquanto isso, aplique as mesmas operações na matriz identidade ao lado.
Passo 3: A matriz inversa é a matriz que se formou no lado direito do algoritmo.
Propriedades da matriz inversa
Pra finalizar algumas propriedades da matriz inversa que volta e meia aparecem nas provas:
- ESSA É MUITO IMPORTANTE!!!
Invertendo matrizes 2 × 2
Invertendo matrizes 3 × 3 e ordem maiores
Propriedades da matriz inversa
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 127 – Prob. 4.13 (Adaptado)
Inverta:
Passo 1
Letra
Como se trata de uma matriz , vamos utilizar o método prático.
Primeiro, vamos trocar os elementos da diagonal principal de lugar e depois multiplicar por a diagonal secundária:
Agora, falta calcular o determinante da matriz original:
E dividir por esse valor:
E pronto, temos a inversa agora.
Passo 2
Letra
Como é de ordem maior que , precisamos utilizar o método de escalonamento.
E a matriz inversa é:
Passo 3
Letra
Vamos utilizar o mesmo principio da letra anterior.
E a matriz inversa é:
Resposta
Exercício Resolvido #2
UFRJ-P4-2015.2.1-08
Calcule a terceira coluna da inversa da matriz:
Passo 1
Agora vem um macete matador pra esse tipo de questão! Como ele só quer descobrir a terceira coluna da matriz inversa nós não precisamos da inversa inteira do outro lado! É só botarmos a terceira. Ou seja, temos que nos preocupar com duas colunas a menos ;)
Passo 2
Passo 3
E assim a terceira coluna da nossa matriz inversa é:
E com isso podemos ver que a terceira coluna é:
Resposta
Letra
Exercício Resolvido #3
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 128 – Fix. 4.21
Se são invertíveis e , então
Passo 1
Bom, o que temos ali é o isolado, então vamos fazer isso. Só que para fazer isso usando a equação que nos foi dada , temos que multiplicar dos dois lados à DIREITA por :
Logo a resposta é a ultima opção.
Resposta
Letra D)
Exercício Resolvido #4
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 128 – Fix. 4.20
A matriz possui inversa . Determine e tais que:
Sendo
Passo 1
Caramba nós só temos a matriz inversa, então vamos ter q inverter de novo para ajeitar tudo??? Claro que não!! Basta ajeitar cada equação:
Letra
Vamos mudar isso um pouco:
Viu, agora é só multiplicar:
Passo 2
Letra
Ajeitando:
Agora é só multiplicar.
Letra
Ajeitando:
Agora é só multiplicar:
Resposta
Exercício Resolvido #5
Elaboração própria
Considere as afirmativas abaixo:
I – Uma matriz é invertível somente se para o sistema a solução for sempre .
II – A inversa da matriz identidade é
III – A matriz é invertível e a sua inversa é triangular superior.
Estão corretas, apenas:
a) I e II
b) I
c) II e III
d) III
e) I, II e III
f) II
g) I e III
Passo 1
Analisando cada uma das afirmativas:
I – Verdadeira. Vamos escrever a equação dada:
Em uma conta normal, passaríamos o pro outro lado dividindo né? Mas quando se trata de matrizes, ele não pode ir dividindo, ele vai como a inversa
Mass, isso só é possível se o for invertível concorda? Assim como o só vai ser invertível se a solução do sistema for essa :)
II – Nananinanão! A inversa da matriz identidade é a própria matriz identidade beleza?
III – Bora lá tentar inverter essa matriz. Colocando ela lado a lado com uma matriz identidade :
Agora é só escalonar a matriz da esquerda até ela se tornar uma matriz identidade:
Opa, na matriz da esquerda ficamos um uma linha de 0’s ali embaixo :( Isso quer dizer que a matriz não é invertível!! Então a afirmativa é falsa ok?
Também poderíamos matar essa afirmativa calculando o determinante da matriz. Como ele é 0, a matriz não é invertível.
Como só a I é verdadeira, a alternativa correta é a letra b
Resposta
b) I
Exercício Resolvido #6
UEMG - Adaptada
Se a inversa de é , qual o valor de ?
Passo 1
Temos uma matriz que possui uma incógnita entre seus termos. Mas ó, a gente tem a inversa dela, o que já ajuda hehe
A gente sabe que , onde é a matriz identidade, então basta resolvermos essa igualdade:
Passo 2
Multiplicando as matrizes:
Igualando os termos da segunda linha e primeira coluna:
(também poderíamos igualar )
Aeee, achamos nosso valor de !! Ele vale 5 :)
Resposta
Exercício Resolvido #7
UNICAMP
Considera a matriz quadrada de ordem :
Onde é um número real.
Podemos afirmar que:
a) não é invertível para nenhum valor de
b) é invertível para um único valor de
c) é invertível para exatamente dois valores de
d) é invertível para todos os valores de
Passo 1
Para sabermos quais os valores de que permitem que seja invertível, vamos calcular o determinante da matriz, lembrando que ele deve ser diferente de 0 certo?
Por relação trigonométrica, temos que
Logo
Opa, nosso determinante sempre vai ser , que é diferente de :O então, nossa matriz sempre vai ser invertível, independente do valor de que estiver ali.
A resposta correta é a letra d ;)
Resposta
d) é invertível para todos os valores de
Exercício Resolvido #8
UNICAMP
Considera a matriz dada:
Onde e são números reais. Se e é invertível, então:
a) e
b) e
c) e
d) e
Passo 1
Vamos começar pela primeira condição: sabemos que
Agora vamos multiplicar pela inversa de , já que o enunciado nos disse que é invertível
Passo 2
O lado direito é mole, né? É só escrever
Que é a definição de inversa mesmo haha
Já o lado esquerdo a gente reescreve da seguinte maneira
Reconhece essa paradinha entre parênteses? É a própria identidade \o/
Isso significa que
Passo 3
Voltando pra aquela equação que tínhamos escrito antes
Ou seja, é a própria identidade ! Show!
O enunciado diz que é assim
Como é a identidade
Vamos ter que e .
Feshow? ;)
Resposta
b) e