Sistema Linear
Teoria
Olá gente bonita, nós somos o Responde Aí, a plataforma de exatas que vai salvar o seu semestre!
Vem com a gente aprender sistemas lineares e como resolvê-los.
Sistema Linear
Um sistema linear é um conjunto de duas ou mais equações, com duas ou mais incógnitas, nas quais só estão envolvidas operações básicas como soma, substração, multiplicação e divisão.
Um exemplo de sistema linear é esse aqui:
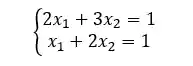
A resolução de sistemas lineares é uma tarefa comum nas áreas das ciências da natureza e da matemática, por esse motivo é bem importante que a gente saiba resolver um sistema linear.
Representação Matricial
Antes da gente focar em como resolver o sistema, vamos entender como a gente pode representar um sistema linear usando as matrizes.
O sistema linear pode ser escrito da seguinte forma:
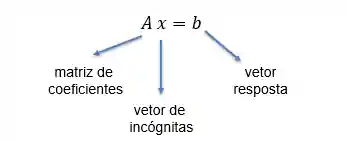
Vamos entender com calma isso aí. Vamos pegar como exemplo aquele sistema linear que vimos lá no início.
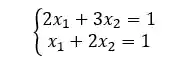
O vetor
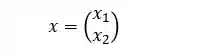
A matriz de coeficientes,
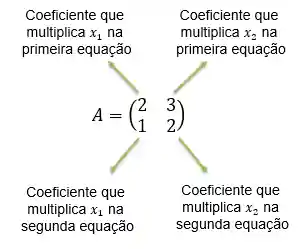
E o vetor de resposta,
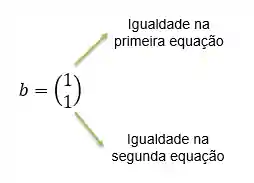
Essas duas formas de representar o sistema são equivalentes:
Há uma outra matriz importante, que chamamos de matriz aumentada. Ela é quase igual à matriz de coeficientes, só que com uma coluna a mais. Nessa última coluna, à direita, colocamos o vetor b.
Veja só a matriz aumentada do sistema que mostramos acima:
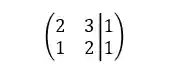
Resolução de um sistema linear
A resolução de um sistema linear pode ser feita através de diversos métodos, mas vamos focar aqui no método de escalonamento, no qual usamos a representação matricial para resolver o problema.
Para entender esse método vamos pegar um exemplo:
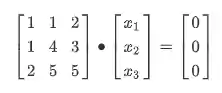
O que vamos fazer é pegar a matriz aumentada desse sistema:
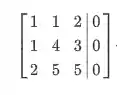
E escalonar ela.
📢 ALERTA: É muito muito muito importante que você saiba escalonar uma matriz para conseguir resolver o sistema linear por esse método. Então, se você ainda não sabe ou tem dúvidas corre pra essa página aqui: Escalonamento
Quando escalonamos essa matriz aumentada obtemos a seguinte matriz:
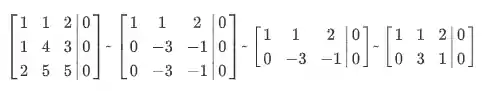
Agora, vamos pegar a matriz escalonada e trazer de volta para a representação em equações. Desse jeito aqui:
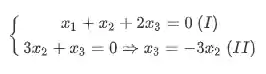
Agora podemos pegar a equação
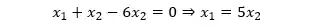
Veja que tanto
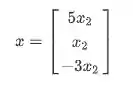
E prontinhos resolvemos nosso sistema linear.
Tranquilo não é?
Uma última observação importante sobre os sistemas lineares. Quando o vetor
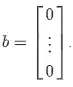
dizemos que o sistema linear é homogêneo.
Fechamos aqui nosso papo de hoje. Praticar é o que você deve fazer agora, por isso eu vou deixar aqui em baixo um vídeo de um exercício resolvido passo-a-passo, de modo que você consegue entender muito bem tudo que precisa fazer para resolver o exercício e mandar super bem na prova. Confere aí 👇🏾
Exercício em vídeo
Confere esse exercício em vídeo, no qual a resolução é feita passo-a-passo junto com você. Aproveita 😉
Resolução de um sistema linear
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 58 – Fix 2.3. Adaptado.
Mostre que o conjunto solução do sistema :
não irá se alterar se acrescentarmos a equação ___ (não resolva o sistema!)
Passo 1
No enunciado foram dadas duas equações com duas incógnitas.
Neste problema, queremos encontrar outra equação para o sistema de modo que o conjunto solução não sofra mudanças.
Temos que lembrar que como vamos ter equações para incógnitas, a terceira equação será obrigatoriamente uma das outras, desse modo, as equações vão ser equivalentes. Para resolver utilizaremos apenas os coeficientes das equações.
Passo 2
Utilizando APENAS os coeficientes:
Vamos escrever os vetores dos coeficientes das equações que temos
Escrevendo o vetor que corresponde aos coeficientes que queremos obter:
Agora vamos escrever uma combinação linear dos dois vetores do sistema e igualar com os da equação que queremos obter. Iremos fazer isso para obter a combinação linear de todos os coeficientes do sistema, beleza?!
Beleza?!
Desse modo temos nossa combinação linear dos coeficientes do sistema!
Passo 3
Vamos encontrar os valores de e :
Da combinação linear obtemos duas equações:
Fazendo as continhas, obtemos:
Ok, podemos ver que irá satisfazer a equação. Assim, para ela ser verdadeira, devemos impor essas condições igual ao que temos no enunciado. Para isso, vamos utilizar a equação que queremos incluir e fazer a combinação linear utilizando os valores de e encontrados.
A primeira equação é igual a 3 e a segunda igual a 1, então vamos escrever uma combinação linear entre esses valores e :
É só pensar na matriz dos coeficientes, beleza?! Se tivermos uma linha redundante, podemos eliminá-la na hora do escalonamento, e não influenciará em nada a solução do nosso sistema :D
Resposta
Exercício Resolvido #2
Prob 2.7, letra b, do livro “Curso de Álgebra Linear – Fundamentos e Aplicações”, de Marco Cabral e Paulo Goldfield
Resolva o sistema linear abaixo, escrevendo o conjunto-solução em equações paramétricas:
Passo 1
Vamos achar a matriz aumentada do sistema.
Lembra que pra fazer isso a gente coloca a matriz dos coeficientes do lado esquerdo e os números que estão depois do igual como um vetor do lado direito.
Agora vamos escaloná-la, seguindo um passo a passo!
Passo 2
- ENCONTRAR O PIVÔ DA PRIMEIRA LINHA
- ZERAR A PRIMEIRA COLUNA (USANDO O PIVÔ DA PRIMEIRA LINHA)
- ENCONTRAR O PIVÔ DA SEGUNDA LINHA
- ZERAR A SEGUNDA COLUNA (USANDO O PIVÔ DA SEGUNDA LINHA)
Qual o primeiro elemento não-nulo da primeira linha?
É o !
Encontrado.
Passo 3
Aqui você precisa zerar o e o que estão logo abaixo do pivô.
Fazendo e , temos o seguinte:
Passo 4
O primeiro elemento não nulo da segunda linha é o .
Peraí, tem algum jeito de transformar logo esse pivô em ?
Claro! Vamos dividir a segunda linha toda por , fazendo .
Passo 5
Agora queremos zerar o logo abaixo do pivô.
Fazendo :
Podemos descartar a linha nula!
Pronto! Está em sua forma escalonada.
Assim, passando para a forma de sistema:
Isolando na primeira equação e na segunda temos:
E
Substituindo o valor de na primeira equação temos:
Logo temos:
A equação vetorial fica:
Que é uma reta no .
Como o problema pede a equação paramétrica, teremos:
,
Resposta
,
Exercício Resolvido #3
Lista 1 de exercícios, 2015.2, exercício 4, Álgebra Linear, PUC-rio
Considere o sistema linear
- Encontre todas as soluções do sistema homogêneo associado e represente este espaço de soluções como um espaço gerado.
- Verifique que é solução do sistema não-homogêneo acima.
- Enconte todas as soluções e represente-as como um espaço gerado deslocado da origem.
Passo 1
Letra : Primeiro escrevemos o sistema homogêneo:
Passo 2
Multiplicando as matrizes e igualando os elementos, temos o sistema:
Passo 3
Substituindo a equação nas equações e , temos o sistema:
Passo 4
Então, o vetor solução desse sistema é o vetor que possui na primeira coordenada, na segunda coordenada e na terceira coordenada. Logo, nosso vetor é:
Sendo a solução do sistema homogêneo, então
Passo 5
Letra : para verificar se o vetor é solução do sistema, basta substitui-lo na forma matricial ou no sistema linear gerado. No caso, a multiplicação de matrizes fica:
Como a multiplicação satisfez a equação matricial, o vetor realmente é solução do sistema.
Passo 6
Letra : o que o problema quer dizer com todas as soluções seria a solução geral, que é:
No caso:
E então:
Resposta
- é solução
Exercício Resolvido #4
Sistemas Lineares
O sistema linear admite a solução . A soma de é:
(a)
(b)
(c)
(d)
Passo 1
Para resolver o sistema, vamos escalonar a matriz aumentada:
Passo :
Passo : e
Passo :
Passo 2
Tendo a matriz escalonada, vamos fazer a substituição para trás:
Na segunda linha:
Na primeira linha:
Passo 3
Com isso, achamos o vetor-solução!
Assim, a soma .
Resposta
(b)
Exercício Resolvido #5
INSTITUTO FEDERAL DO MATO GROSSO, Álgebra Linear – Sistemas Lineares, Professor Rogério Matos - Adaptado
Resolva o sistema abaixo pelos métodos pedidos.
a) Método da substituição.
b) Método da adição.
c) Escalonamento.
Passo 1
Bom, a gente viu lá na teoria que tem 3 métodos possíveis pra resolver um sistema, que são esses das letras a, b e c certo?
Então a gente vai usar cada um deles pra resolver o mesmo sistema, vamos lá :D
Passo 2
a) Substituição
Da segunda linha do sistema, podemos isolar , ficando com
Beleza, a gente ficou com em função de né?
Agora vamos substituir isso na primeira equação, no lugar de :
Opa, agora a gente tem uma equação em função apenas de !! É só resolver pra encontrar o valor dele:
Boa, agora, a gente viu ali em cima que , então:
E fimmm, encontramos que e pelo método da substituição :P
Passo 3
b) Adição
O principal objetivo na adição é somar as duas equações de modo que isso suma com uma das incógnitas. Então, por exemplo, se multiplicarmos a segunda equação por , vamos ter:
Entendeu? Quis deixar o com o mesmo coeficiente (só que com sinais opostos) em cima e embaixo ;)
Outra opção seria multiplicar em cima por e embaixo por , porque aí ficaria em cima e embaixo.
Continuando, agora vamos somar as duas equações:
Aeee, já achamos o , agora é só substituir em uma das equações pra achar o . Substituindo na primeira:
É isso aí! Encontramos e do nosso sistema pelo método da adição e como esperado, deu o mesmo valor que pelo método da substituição :)
Passo 4
c) Escalonamento
Agora vem o famoso escalonamento hehe primeiro vamos colocar nosso sistema em formato de matriz aumentada:
Agora vamos escalonar daquele jeitinho que aprendemos:
Opa essa foi fácil hahaha agora, voltando ao sistema com os novos coeficientes:
Da segunda linha, temos que
Substituindo na primeira linha:
E é isso, resolvemos o sistema por escalonamento e conseguimos o mesmo resultado dos outros métodos :) lembrando que o que mais vamos utilizar é escalonamento ok?
Resposta
e
Exercício Resolvido #6
UESP
Se o termo é a solução do sistema abaixo, então é igual a:
a) -8
b) -7
c) -6
d) -5
e) -4
Passo 1
Aqui nós vamos primeiro resolver nosso sistema, pra encontrarmos a solução . Depois, vamos substituir esses valores na conta pra encontrarmos nosso resultado beleza?
Nosso sistema é o seguinte
Ele pode ser escrito na seguinte matriz aumentada:
Agora podemos resolver por escalonamento :)
Passo 2
Escalonando nossa matriz:
Boa, nossa matriz está escalonada :D
Agora podemos escrever como sistema novamente:
Passo 3
Do sistema obtido, temos na última linha que:
Substituindo na segunda linha:
Substituindo na primeira linha:
Então, nossa solução é .
Agora é só substituir naquela conta:
Aeee, então a alternativa correta é a letra B :)
Resposta
b) -7
Exercício Resolvido #7
IME – USP, Exercícios de álgebra linear
Se
Encontre , , e .
Passo 1
O primeiro passo aqui é igualarmos cada termo das matrizes. Assim, o termo da primeira matriz é igual o termo da segunda e por aí vai, isso vai nos dar o sistema:
Boa, agora é só resolvermos esse sistema :)
Passo 2
Podemos resolver esse sistema pos substituição.
Como assim???
Olha, na terceira equação podemos isolar o , isso vai nos dar
Ok, agora podemos substituir na segunda equação:
Aí, já achamos o :)
Como sabemos que :
Passo 3
Substituindo na quarta equação, temos
Substituindo na primeira equação:
Então achamos todas as nossas incógnitas :D
Resposta
Exercício Resolvido #8
Universidade do Algarve, Exercícios de Álgebra Linear e Geometria Analítica
Um biólogo colocou três espécies de bactérias (denotadas por I, II e III) num tubo de ensaio, onde elas serão alimentadas por três fontes diferentes de alimentos (A, B e C). Em cada dia serão colocadas no tubo de ensaio 1500 unidades de A, 3000 unidades de B e 4500 unidades de C. Cada bactéria consome um certo número de unidades de cada alimento por dia, como mostra a tabela. Quantas bactérias podem coexistir no tubo de ensaio de modo a consumir todo o alimento?
Passo 1
Vamos chamarde a bactéria I, a bactéria II e a bactéria III.
Com os valores dados no enunciado e os coeficientes da tabela, construímos o sistema:
Boaa, agora é só resolver esse sistema pra vermos quantas bactérias podemos ter no tubo para consumir todo o alimento hehe
Passo 2
Escrevendo nosso sistema como uma matriz aumentada:
Agora vamos escalonar:
Opa, uma das linhas foi anulada, vamos voltar pro sistema pra ver o que fazemos.
Passo 3
Voltando ao sistema com os novos coeficientes:
Bom, se uma das linhas foi anulada, já sabemos que uma das respostas vai ser um parâmetro.
Escolhendo como parâmetro, vamos isolar na segunda linha e assim teremos
Substituindo na primeira linha:
Então:
Logo, nesse sistema, pode assumir qualquer valor, enquanto e variam em função dele. Temos infinitas soluções :D
Resposta
Exercício Resolvido #9
UFG, Lista de exercícios de Álgebra Linear - Adaptado
Utilize escalonamento para resolver o seguinte sistema de equações.
Passo 1
Antes de começar a escalonar, temos que colocar esse sistema em uma matriz aumentada:
Escalonando:
Opa, a segunda e a terceira linha ficaram iguais :O então podemos escrever a matriz aumentada assim:
Passo 2
Passando a matriz aumentada de volta para um sistema:
Se isolarmos na segunda equação, teremos:
Agora vamos substituir isso na primeira equação:
Isolando :
Passo 3
Beleza, nosso conjunto solução é .
Mas no passo 2 vimos que e .
Então nosso conjunto solução se torna:
Quee! Que negócio confuso!
Calma, vamos separar as variáveis em partes diferentes:
Colocando os parâmetros em evidência:
Logo, temos infinitas soluções nesse sistema, sendo uma combinação linear com 3 parâmetros, onde , e variam livremente.