Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Ângulo entre Planos

Ver Todos os Exercícios

Teoria

Como calcular ângulo entre planos?

Calma, não faz essa cara não, vou te ensinar agora como encontrar!

Imagina que temos dois planos se cruzando fazendo um ângulo como mostra a figura:

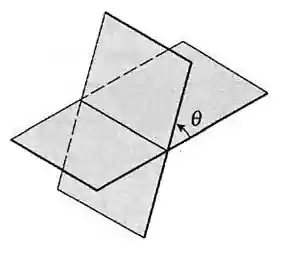
Dois planos formando um ângulo theta
Dois planos formando um ângulo theta

Calcular esse ângulo é bem simples, bastanta sabermos os vetores normais de cada um dos planos e usar a seguinte fórmula:

Vamos fazer um exemplo juntos para você entender.

Qual é o ângulo entre os planos: e ?

Primeiro vamos escrever os vetores normais a cada plano. Olhando a equação dos planos, temos:

Agora, vamos fazer o produto interno entre esses vetores:

Agora, vamos calcular os módulos desses vetores normais:

Agora é só colocar tudo na fórmula:

E prontinho, achamos o ângulo entre planos!

Agora é só praticar com todos os exercícios resolvidos que temos e ficar expert no assunto! 😉

Exercícios Resolvidos

Exercício Resolvido #1

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 212-1.

Ache a medida θ do ângulo entre os planos

π 1 : x - y + z = 20       e       π 2 : x + y + z = 0

Passo 1

Já calculamos ângulo entre reta e ângulo entre reta e plano! Chegou a vez de calcular o ângulo entre planos!! Chegou a hora de resolvermos o problema lá da teoria, lembra?? Da rampa de acesso para cadeirante!! ;)

O enunciado nos fornece os dados como queremos, ou seja, a equação geral dos planos para que já possamos tirar qua lo vetor normal deles.

Passo 2

Primeiro, vamos retirar das equações qual o vetor normal de cada plano:

n 1 → = 1 ,   - 1 ,   1

n 2 → = 1 ,   1 ,   1

Tendo os vetores, vamos ver o que precisamos para usar a fórmula:

cos ⁡ θ = n 1 → ∙ n 2 → n 1 → | n 2 → |

Passo 3

Olhando a fórmula precisamos do módulo do produto escalar entre os vetores, e o módulo deles:

n 1 → ∙ n 2 → = 1 ,   - 1 ,   1 ∙ 1 ,   1 ,   1 = | 1 - 1 + 1 | = 1

n 1 → = 1 2 + ( - 1 ) 2 + 1 2 = 3

| n 2 → | = 1 2 + 1 2 + 1 2 = 3

Colocando os valores na fórmula, temos:

cos ⁡ θ = n 1 → ∙ n 2 → n 1 → n 2 → → cos ⁡ θ = 1 3 3 = 1 3

θ = cos - 1 ⁡ 1 3

Resposta

θ = cos - 1 ⁡ 1 3

Exercício Resolvido #2

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 183-33b.

Determinar o ângulo entre os planos

π 1 : 2 x - 2 y + 1 = 0       e       π 2 : 2 x - y - z = 0

Passo 1

Olhando para equação desses planos, já podemos pegar os vetores normais!

n 1 → = 2 ,   - 2 ,   0

n 2 → = 2 ,   - 1 ,   - 1

Tendo os vetores, vamos ver o que precisamos para usar a fórmula:

cos ⁡ θ = n 1 → ∙ n 2 → n 1 → | n 2 → |

Passo 2

Olhando a fórmula precisamos do módulo do produto escalar entre os vetores, e o módulo deles:

n 1 → ∙ n 2 → = 2 ,   - 2 ,   0 ∙ 2 ,   - 1 ,   - 1 = | 4 + 2 + 0 | = 6

n 1 → = 2 2 + ( - 2 ) 2 + 0 2 = 8

| n 2 → | = 2 2 + ( - 1 ) 2 + ( - 1 ) 2 = 6

Colocando os valores na fórmula, temos:

cos ⁡ θ = n 1 → ∙ n 2 → n 1 → n 2 → → cos ⁡ θ = 6 8 6 = 6 48 = 3 2 3 = 3 2

θ = cos - 1 ⁡ 3 2 = 30 °

Resposta

θ = 30 °

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 183-33c.

Determinar o ângulo entre os planos

π 1 : 3 x + 2 y - 6 = 0       e       π 2 : p l a n o   x O z

Passo 1

Bom, do plano π 1 eu sei o vetor normal!

n 1 → = 3 ,   2 ,   0

Mas e o vetor normal de π 2 ??

Pensa comigo, galera. O plano x O z é formado por um vetor diretor da reta do eixo x e um vetor diretor da reta do eixo z :

Então se nós fizermos o produto vetorial entre   x → e   z → , vamos obter um vetor perpendicular a eles, ou seja, um vetor normal ao plano!

Considerando   x → = 1 ,   0 ,   0 e   z → = ( 0 ,   0 ,   1 ) , temos:

x → × z → = i → j → k → 1 0 0 0 0 1 = ( 0 ,   - 1 ,   0 )

Logo,   n 2 → = ( 0 ,   - 1 ,   0 )

Passo 2

Agora é só completar a fórmula!

cos ⁡ θ = n 1 → ∙ n 2 → n 1 → | n 2 → |

Calculando os termos:

n 1 → ∙ n 2 → = 3 ,   2 ,   0 ∙ 0 ,   - 1 ,   0 = | 0 + ( - 2 ) + 0 | = 2

n 1 → = 3 2 + 2 2 + 0 2 = 13

| n 2 → | = 0 2 + ( - 1 ) 2 + 0 2 = 1

Colocando os valores na fórmula, temos:

cos ⁡ θ = n 1 → ∙ n 2 → n 1 → n 2 → → cos ⁡ θ = 2 1 13 = 2 13

θ = cos - 1 ⁡ 2 13

Resposta

θ = cos - 1 ⁡ 2 13

Exercício Resolvido #4

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 183-34.

Determinar o valor de m para que seja de 30 ° o ângulo entre os planos

π 1 : x + m y + 2 z - 7 = 0       e       π 2 : 4 x + 5 y + 3 z - 2 = 0

Passo 1

Tudo igual por enquanto! Vamos determinar os vetores normais:

n 1 → = 1 ,   m ,   2

n 2 → = ( 4 ,   5 ,   3 )

Passo 2

Agora a gente olha para fórmula e reflete

cos ⁡ θ = n 1 → ∙ n 2 → n 1 → | n 2 → |

Refletiu?

Beleza, vamos em frente haha

Calculando os termos normalmente:

n 1 → ∙ n 2 → = 1 ,   m ,   2 ∙ 4 ,   5 ,   3 = 4 + 5 m + 6 = 10 + 5 m

n 1 → = 1 2 + m 2 + 2 2 = 5 + m 2

| n 2 → | = 4 2 + 5 2 + 3 2 = 50

O moço quer que o ângulo seja de 30 ° , logo cos ⁡ 30 = 3 2

Colocando os valores na fórmula, temos:

cos ⁡ θ = n 1 → ∙ n 2 → n 1 → n 2 → → 3 2 = 10 + 5 m 50 5 + m 2

3 2 = 10 + 5 m 250 + 50 m 2

Multiplicando cruzado,

750 + 150 m 2 = 20 + 10 m

Elevando os dois lados ao quadrado

750 + 150 m 2 = 400 + 400 m + 100 m 2

50 m 2 - 400 m + 350 = 0

Dividindo por 50

m 2 - 8 m + 7 = 0

m - 1 m - 7 = 0

Logo, m = 1 ou m = 7

Resposta

m = 1   o u   m = 7

Exercício Resolvido #5

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 213-2.

Obtenha uma equação geral do plano π , que contém a reta

r :   x - 2 y + 2 z = 0 3 x - 5 y + 7 z = 0

E forma com o plano π 1 : x + z = 0 um ângulo de 60 ° .

Passo 1

Nossa!! Não sei nem por onde começar!!

Calma, pequeno gafanhoto!! Vamos por partes!!

Primeiro, se a gente olhar para forma em que a reta r está escrita, vamos ver que ela é formada pela intereseção de dois planos, sendo eles (os planos):

x - 2 y + 2 z = 0 3 x - 5 y + 7 z = 0

Assim sendo, o plano em que a reta está contida (que é o que queremos descobrir) é a combinação linear dessas duas expressões, ou seja:

α x - 2 y + 2 z + β 3 x - 5 y + 7 z = 0

Essa é a equação geral do plano que queremos descobrir. Escrevendo a equação de forma a isolar as coordenadas, temos:

x α + 3 β + y - 2 α - 5 β + z 2 α + 7 β = 0

Passo 2

Com a expressão x α + 3 β + y - 2 α - 5 β + z 2 α + 7 β = 0 sabemos que os coeficientes da equação geral do plano que queremos descobrir é:

a = α + 3 β

b = - 2 α - 5 β

c = 2 α + 7 β

d = 0

Com essas informações conseguimos obter as coordenadas do vetor normal ao plano!

n → = ( α + 3 β ,   - 2 α - 5 β ,   2 α + 7 β )    

Passo 3

Agora, para descobrimos o valor de α e β vamos usar a segunda informação que temos: que o plano π forma 60 ° com o plano π 1 . A fórmula do ângulo entre planos é:

cos ⁡ θ = n 1 → ∙ n → n 1 → | n → |

Temos:

n → = ( α + 3 β ,   - 2 α - 5 β ,   2 α + 7 β )    

n 1 → = ( 1 ,   0 ,   1 )

θ = 60 ° → cos ⁡ 60 ° = 1 2

Calculando o produto interno entre os vetores normais e o módulo dos vetores:

n 1 → ∙ n 2 → = ( α + 3 β ,   - 2 α - 5 β ,   2 α + 7 β )     ∙ 1 ,   0 ,   1 = | α + 3 β + 2 α + 7 β | = | 3 α + 10 β |

n → = ( α + 3 β ) 2 + ( - 2 α - 5 β ) 2 + ( 2 α + 7 β ) 2 = 9 α 2 + 54 α β + 83 β 2

n 1 → = 1 2 + 1 2 = 2

Subsituindo na fórmula,

cos ⁡ θ = n 1 → ∙ n → n 1 → | n → | → 1 2 = 3 α + 10 β 2 9 α 2 + 54 α β + 83 β 2

Elevando os dois lados ao quadrado, chegamos na igualdade:

3 α 2 + 22 α β + 39 β 2 = 0

Resolvendo a equação de 2º grau acima em α , chegaremos que:

α = - 3 β           o u             α = - 13 3 β

Passo 4

Agora que temos α = - 3 β     o u     α = - 13 3 β , falta substituirmos em:

n → = ( α + 3 β ,   - 2 α - 5 β ,   2 α + 7 β )    

Substituindo α = - 3 β   , teremos:

n → = ( 0 ,   β ,   β )    

S e   β = 1 →   n → = ( 0 ,   1 ,   1 )    

Nossa equação geral do plano será y + z = 0

Já se α = - 13 3 β :

n → = - 4 3 β , 11 3 β ,   - 5 3 β →     n → = - 4 β , 11 β ,   - 5 β  

S e   β = 1 →   n → = ( - 4 ,   11 ,   - 5 )    

Nossa equação geral do plano será - 4 x + 11 y - 5 z = 0 → 4 x - 11 y + 5 z = 0

Assim, nosso plano tem duas equações possíveis:

y + z = 0         e           4 x - 11 y + 5 z = 0

Resposta

y + z = 0         e           4 x - 11 y + 5 z = 0

Exercícios de Livros Relacionados

Verifique se o plano pi separa os pontos A e B .b) A = (1 , 0 , 3) B = (1 , - 1 , - 4) pi : x - y - z = 4
Verifique se o plano pi separa os pontos A e B .a) A = (1 , 2 , 3) B = (0 , - 1 , - 4) pi : x - 3 y - z = 1
Determine a parte da reta r : X = 0 ,0 ,0 + λ . ( 1 ,2 ,1 ) que é visível para um observador situado no ponto ( 1 ,0 ,0 ) , supondo que os planos π 1 : x + y - z - 2 = 0 e π 2 : 2 x - y + z + 2 = 0 se
Verifique se o plano pi separa os pontos A e B .c) A = (0 , 0 , 0) B = (0 , - 1 , - 3) pi : x = 3 y - z - 1
Obtenha uma equação geral do plano que contém r e forma ângulo de θ radianos com π .a) r : x = z + 1 = y + 2 π : x + 2 y - 3 z + 2 = 0 θ = π 3