Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Ângulo entre Reta e Plano

Ver Todos os Exercícios

Teoria

Já vimos ângulo entre retas, mas e para o ângulo entre reta e plano?

°

Deve ter outra fórmula, certo? Exatamente!! Vamos te mostrar como funciona!!

Considerando que nosso plano tenha um vetor normal n → e que nossa reta tenha vetor diretor r → .

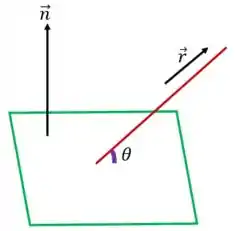
Então a formuleta para encontrar o ângulo θ entre a reta e o plano é:

Aqui também θ varia entre 0 ° e 90 ° .

Vamos fazer um exemplo!

Considere o plano π : 4 x - y + z + 3 = 0 e a reta r : x = t y = 1 + 2 t z = 2 - t . Qual é o ângulo entre eles??

Bem, da equação da reta tiramos   r → = ( 1 ,   2 ,   - 1 ) e da equação do plano, temos   n → = ( 4 ,   - 1 ,   1 )

Vamos fazer o produto interno entre   r → e   n → :

n → ∙ r → = 4 × 1 + - 1 × 2 + 1 × - 1 = 1

E os módulos:

n → = 4 2 + - 1 2 + 1 2 = 18 = 3 2

  r → = 1 2 + 2 2 + - 1 2 = 6

Colocando tudo na fórmula:

sin ⁡ θ = 1 3 2 × 6 = 1 3 12

Logo, θ = sin - 1 ⁡ 1 6 3

UHULLL!!!

Observação: Uma dica para te ajudar a não se confundir com as fórmulas, a fórmula de ângulo entre reta e plano é a única que tem seno, as outras são com cosseno!!

Vamos ficando por aqui! Mas não esquece os exercícios!

Exercícios Resolvidos

Exercício Resolvido #1

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 210-1.

Ache a medida em radianos do ângulo entre

r : X = 0 ,   1 ,   0 + λ ( - 1 ,   - 1 ,   0 ) e π : y + z - 10 = 0

Passo 1

Nesse exercício temos uma reta r e um plano π . Queremos descobrir qual a medida do ângulo entre eles, mas em radianos.

Bora começar então!!

Passo 2

Pela teoria sabemos que para encontrar o ângulo entre um plano e uma reta, precisamos do vetor diretor da reta E do vetor normal ao plano. Vamos retirar esses dados das equações que temos, então:

r → = - 1 ,   - 1 ,   0

n → = ( 0 ,   1 ,   1 )

A fórmula para calcular θ o ângulo entre o plano e a reta é:

sin  ⁡ θ = r → ∙ n → r → | n → |

Passo 3

Antes de colocar tudo na fórmula, vamos calcular separadamente o módulo do produto escalar e o módulo dos vetores:

r → ∙ n → = - 1 ,   - 1 ,   0 ∙ 0 ,   1 ,   1 = | 0 - 1 + 0 | = 1

r → = ( - 1 ) 2 + ( - 1 ) 2 = 2

n → = 1 2 + 1 2 = 2

Agora que já temos os valores só colocar na fórmula:

sin  ⁡ θ = r → ∙ n → r → | n → | → sin ⁡ θ = 1 2

θ = 30 °

Mais uma vez, queremos o resultado em radianos, então:

θ = π 6   r a d

Resposta

θ = π 6   r a d

Exercício Resolvido #2

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 211-2.

Obtenha equações paramétricas da reta r , que passa pelo ponto P = ( 1 ,   1 ,   1 ) , é paralela ao plano π 1 : x + 2 y - z = 0 , e forma com o plano π 2 : x - y + 2 z = 1 um ângulo de π 3 r a d .

Passo 1

Cada vez mais nossos exercício vão ficam mais interessantes!! Vamos ver como se faz esse??

Isso aí!! Quero ver entusiasmo!! Rsrs

O enunciado nos pede para escrevermos as equações paramétricas da reta r !! Mas, o que sabemos sobre ela??

Sabemos que ela passa pelo ponto P = ( 1 ,   1 ,   1 ) . Que é paralela ao plano π 1 e que forma com o plano π 2 um ângulo de π 3 r a d .

Passo 2

Vamos por partes!! O ponto P vai nos ajudar a escrever as equações paramétricas, pois para isso precisamos de um ponto que passa pela reta!! Então, o ponto temos!! Precisamos achar o vetor diretor da reta!!

Para isso, usaremos as outras duas informações que temos. Vamos começar com a informação sobre o paralelismo com o plano   π 1 .

Se a reta r é paralela ao plano π 1 , então isso significa que o vetor diretor de r   ( r → ) é ortogonal ao vetor normal do plano   π 1   ( n 1 → )   , ou seja:

r → ∙ n 1 → = 0

Então, se dissermos que r → = ( a ,   b ,   c ) e sabemos que n 1 → = ( 1 ,   2 ,   - 1 ) retirado da equação geral do plano     π 1 , temos:

a ,   b ,   c ∙ 1 ,   2 ,   - 1 = 0 → a + 2 b - c = 0 → c = a + 2 b

Passo 3

Pronto, já temos uma relação!! Agora falta achar a segunda relação!! Essa acharemos por meio do que temos de informação sobre o plano π 2 .

Do plano π 2 temos que n 2 → = ( 1 ,   - 1 ,   2 ) e que ele forma π 3 r a d com r . Então, temos a fórmula do ângulo entre reta e plano:

sin  ⁡ θ = r → ∙   n 2 → r → |   n 2 → |

Temos:

sin ⁡ π 3 = 3 2

r → ∙   n 2 → = a ,   b ,   c ∙ 1 ,   - 1 ,   2 = | a - b + 2 c |

r → = a 2 + b 2 + c 2

n 2 → = 1 2 + ( - 1 ) 2 + 2 2 = 6

Colocando na fórmula temos:

sin  ⁡ θ = r → ∙   n 2 → r → |   n 2 → | →   3 2 = a - b + 2 c 6 a 2 + b 2 + c 2

Do Passo 2, temos a relação c = a + 2 b , substituindo:

3 2 = a - b + 2 ( a + 2 b ) 6 a 2 + b 2 + ( a + 2 b ) 2

3 6 a 2 + b 2 + ( a + 2 b ) 2 = 2 a - b + 2 ( a + 2 b )

Elevando os dois lados ao quadrado, temos:

3.6 . a 2 + b 2 + a + 2 b 2 = 4 ( 3 a + 3 b ) 2

18 a 2 + b 2 + a 2 + 4 a b + 4 b 2 = 4 9 a 2 + 18 a b + 9 b 2

36 a 2 + 72 a b + 90 b 2 = 36 a 2 + 72 a b + 36 b 2

54 b 2 = 0 → b = 0

Se b = 0 , pela relação do Passo 2 temos:

c = a + 2 b → c = a

Logo, r → = a ,   0 ,   a .

Passo 4

Escolhendo a = 1 ,

r → = 1 ,   0 ,   1

Agora temos r → = 1 ,   0 ,   1 e o ponto P = ( 1 ,   1 ,   1 ) . Já podemos escrever a equação paramétrica da reta r :

r :   x = 1 + t y = 1 z = 1 + t

Ufa!!! Essa foi boa, mas longa hehe

Resposta

r :   x = 1 + t y = 1 z = 1 + t

Exercício Resolvido #3

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 218-8.

Ache um vetor diretor de uma reta paralela ao plano π : x + y + z = 0 e que forma 45 graus com o plano π 1 : x - y = 0 .

Passo 1

Mais um e acabou!!

Bora fazer para fechar esse tópico com chave de ouro!! Haha

O enunciado nos pede para determinar o vetor diretor de uma reta. Sendo que, essa reta é paralela ao plano π e forma 45 ° com o plano   π 1 . Vamos tirar as informações que temos:

π :   n → = 1 ,   1 ,   1   e   p a r a l e l o   à   r e t a

  π 1 :   n 1 → = 1 ,   - 1 ,   0 e   f o r m a   45 °   c o m   a   r e t a

r e t a :   r → = ( a ,   b ,   c )

Passo 2

Vamos começar com os dados que temos do plano π ! Como esse plano é paralelo à reta, sabemos que :

  n → ∙ r → = 0

Então, teremos:

1 ,   1 ,   1 ∙ a ,   b ,   c = a + b + c = 0

a + b + c = 0 → c = - a - b

Temos uma primeira relação.

Passo 3

A segunda relação iremos tirar das informações sobre o plano   π 1 ! Sabemos que a fórmula do ângulo entre reta e plano é:

sin  ⁡ θ = r → ∙   n 1 → r → |   n 1 → |

Temos,

sin ⁡ 45 ° = 2 2

r → ∙   n 1 → = a , b ,   c ∙ 1 ,   - 1 ,   0 = | a - b |

r → = a 2 + b 2 + c 2

| n 1 | → = 1 2 + ( - 1 ) 2 = 2

Subsituindo os valoers na fórmula:

sin  ⁡ θ = r → ∙   n 1 → r → |   n 1 → | →   2 2 = a - b 2 a 2 + b 2 + c 2

Substituindo c = - a - b :

2 2 = a - b 2 a 2 + b 2 + ( - a - b ) 2

Resolvendo:

a 2 + 4 a b + b 2 = 0

Resolvendo a equação do 2º grau em a , teremos:

a = - 2 b ± b 3

S e   b = 1 → a = - 2 ± 3

Substituindo c = - a - b :

S e   a = - 2 + 3 → c = 1 - 3

S e   a =   - 2 - 3 → c = 1 + 3

Então, teremos duas retas, com vetores diretores:

- 2 + 3 ,   1 ,   1 - 3         e           ( - 2 - 3 ,   1 ,   1 + 3 )

Resposta

- 2 + 3 ,   1 ,   1 - 3         e           ( - 2 - 3 ,   1 ,   1 + 3 )

Exercício Resolvido #4

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 173-12.

Determinar o ângulo que a reta

r : x = 1 - 2 t y = - t z = 3 + t faz com o plano π : x + y - 5 = 0

Passo 1

Pela teoria sabemos que para encontrar o ângulo entre um plano e uma reta, precisamos do vetor diretor da reta E do vetor normal ao plano. Vamos retirar esses dados das equações que temos, então:

r → = - 2 ,   - 1 ,   1

n → = ( 1 ,   1 ,   0 )

A fórmula para calcular θ o ângulo entre o plano e a reta é:

sin  ⁡ θ = r → ∙ n → r → | n → |

Passo 2

Antes de colocar tudo na fórmula, vamos calcular separadamente o módulo do produto escalar e o módulo dos vetores:

r → ∙ n → = - 2 ,   - 1 ,   1 ∙ 1 ,   1 ,   0 = | - 2 - 1 + 0 | = 3

r → = ( - 2 ) 2 + ( - 1 ) 2 + 1 2 = 6

n → = 1 2 + 1 2 = 2

Agora que já temos os valores só colocar na fórmula:

sin  ⁡ θ = r → ∙ n → r → | n → | → sin ⁡ θ = 3 6 × 2

sin ⁡ θ = 3 12 = 3 2 3

Multiplicando por 3 3 ,

sin ⁡ θ = 3 3 2 × 3 = 3 2

θ = 60 °

Se você preferir o resultado em radianos, então:

θ = π 3   r a d

Resposta

θ = 60 ° = π 3   r a d

Exercício Resolvido #5

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 174-13.

Verificar se a reta

r : x - 2 3 = y + 1 - 2 = z - 1 é perpendicular ao plano π : 9 x - 6 y - 3 z + 5 = 0

Passo 1

Bem, se a reta e o plano são perpendiculares, o ângulo entre eles tem que ser 90 ° ! Também sabemos que sin ⁡ 90 ° = 1 , então é só usar isso na nossa fórmulinha!

Pela teoria sabemos que para encontrar o ângulo entre um plano e uma reta, precisamos do vetor diretor da reta E do vetor normal ao plano. Vamos retirar esses dados das equações que temos, então:

r → = 3 ,   - 2 ,   - 1

n → = ( 9 ,   - 6 ,   - 3 )

A fórmula é (lembrando que nesse caso θ = 90 ° ):

sin  ⁡ θ = r → ∙ n → r → | n → |

Passo 2

Antes de colocar tudo na fórmula, vamos calcular separadamente o módulo do produto escalar e o módulo dos vetores:

r → ∙ n → = 3 ,   - 2 ,   - 1 ∙ 9 ,   - 6 ,   - 3 = | 27 + 12 + 3 | = 42

r → = 3 2 + ( - 2 ) 2 + ( - 1 ) 2 = 14

n → = 9 2 + ( - 6 ) 2 + - 3 2 = 126

Agora que já temos os valores só colocar na fórmula:

sin  ⁡ θ = r → ∙ n → r → | n → | → sin ⁡ θ = 42 14 × 126

Vamos ver se isso vai dar 1 (já que sin ⁡ 90 ° = 1 )

sin ⁡ θ = 42 1764 = 42 42 = 1

Como achamos que,

sin ⁡ θ = 1

θ = 9 0 °

E a reta e o plano são perpendiculares!

Resposta

θ = 9 0 °

Exercício Resolvido #6

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 174-13.

Determinar o ângulo formado pela reta

r : y = - 2 x z = 2 x + 1 e ao plano π : x - y + 5 = 0

Passo 1

Primeiro, vamos passar a equação da reta para forma simétrica (para facilitar a visualização)!

Vamos escrever as coordenadas em função de x :

r : y = - 2 x → x = y - 2 z = 2 x + 1 → x = z - 1 2

Assim,

r : x = y - 2 = z - 1 2

Passo 2

Pela teoria sabemos que para encontrar o ângulo entre um plano e uma reta, precisamos do vetor diretor da reta E do vetor normal ao plano. Do passo 1 e do enunciado, tiramos:

r → = 1 ,   - 2 ,   2

n → = ( 1 ,   - 1 ,   0 )

A fórmula é:

sin  ⁡ θ = r → ∙ n → r → | n → |

Passo 3

Antes de colocar tudo na fórmula, vamos calcular separadamente o módulo do produto escalar e o módulo dos vetores:

r → ∙ n → = 1 ,   - 2 ,   2 ∙ 1 ,   - 1 ,   0 = | 1 + 2 + 0 | = 3

r → = 1 2 + ( - 2 ) 2 + 2 2 = 9 = 3

n → = 1 2 + ( - 1 ) 2 + 0 2 = 2

Agora que já temos os valores só colocar na fórmula:

sin  ⁡ θ = r → ∙ n → r → | n → | → sin ⁡ θ = 3 3 × 2

sin ⁡ θ = 1 2

Multiplicando por 2 2

sin ⁡ θ = 2 2

θ = 45 °

Resposta

θ = 45 °

Exercícios de Livros Relacionados

Renato inventou o seguinte método para calcular a medida angular θ entre uma reta r e um plano π : escolhe um vetor diretor r → da reta, um vetor n → normal ao plano, determina, em seguida, o vetor u
Sejam r → e s → , respectivamente, vetores diretores das retas r e s . Mostre que um plano π forma ângulos congruentes com essas retas se, e somente se, os comprimentos das projeções ortogonais de cad
Sejam P = ( 1 ,2 ,- 1 ) , Q a projeção ortogonal de R = ( - 1 ,- 1 ,- 2 ) sobre π : x + y + z + 1 = 0 e θ a medida angular entre a reta P Q e π . Calcule cos ⁡ θ .
Obtenha a medida angular em radianos entre a reata r e o plano π .e) r : x - 2 z = y + 2 z = 1π : 45 7 x + y + 2 z - 10 = 0
Obtenha a medida angular em radianos entre a reta r e o plano π .b) r : x = y = z π : z = 0