Introdução à Reta
Produzido por Aline BuzziTeoria
O que é uma reta?
No dia a dia a gente fala que uma reta é qualquer coisa sem curva, contínua, certo? Tipo essa estrada:

Agora imagina uma estrada dessa infinita disposta no plano (em 2D) ou no espaço (em 3D). Opa, como assim?
Quando a gente tem um segmento reto e infinito, vamos chamar ele de reta, então uma reta nada mais é que um vetor infinito! Como assim? Ela tem direção, mas seu tamanho é infinito e não possui um sentido determinado como o vetor, tipo assim ó:
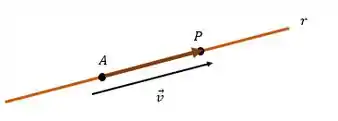
Uma reta possui infinitos pontos e possui uma direção. Os pontos e representam dois dos pontos que pertencem à reta e o vetor indica sua direção.
Bora entender melhor isso aí :P
Retas
Se tivermos uma expressão em três dimensões (ou seja, com três coordenadas):
Sendo qualquer número inteiro.
Vamos tentar colocar esse lugar geométrico em um gráfico pra 3 valores diferentes de , de acordo com a tabela abaixo (a gente só substitui o valor de , multiplica por e faz a soma beleza?):

Colocando os pontos , e no espaço, a gente tem isso aqui:
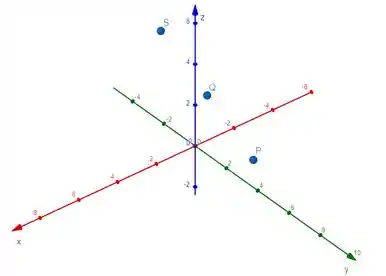
Lembra daquela brincadeira de ligar os pontos? Vamos ligar esses 3 pontos que encontrarmos haha, vamos ter esse segmento preto:
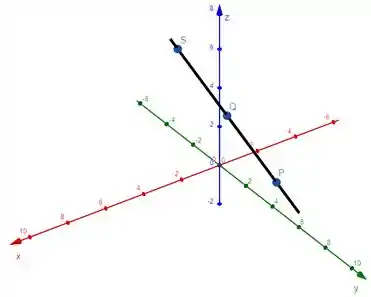
Ta mas e aí que isso?
Esse segmento é a reta , da equação .
Deixa eu te explicar melhor, existem INFINITOS , cada um vai nos dar um pontinho do espaço, e ligando todos os pontos temos o segmento que chamamos de reta, que no caso vai ser infinita também, ali na figura temos apenas uma amostra :P.
O vetor que determina a direção dessa reta pode ser , , , enfim, qualquer vetor que ligue dois pontos dessa reta serve!! Afinal todos eles são paralelos então vão dar a mesma direção pra reta ;)
Equação vetorial de uma reta
A equação que vimos no exemplo () é chamada de equação vetorial da reta.
Pra entender melhor, vamos voltar naquela imagem do comecinho:
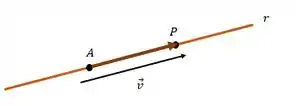
Para que uma reta fique bem definida, o vetor deve ser colinear ao vetor . Para que sejam colineares eles devem ser múltiplos, logo:
Assim, com a expressão acima podemos determinar de qual reta estamos falando. Sendo, um ponto genérico , um ponto conhecido da reta e o vetor diretor.
Assim, na reta podemos ter certeza que ela passa pelo ponto (isso acontece quando ) e que seu vetor diretor é (ou qualquer múltiplo dele).
LEMBRANDO: na nossa equação usamos como parâmetro, mas podemos usar , , qualquer letra (fora , e , pra não confundirmos com as coordenadas).
O formato geral da equação vetorial é:

Para tornar nosso estudo mais simples, sempre usaremos como sendo as coordenadas de um ponto conhecido e as coordenadas do vetor diretor. Blz?
Mas, só tem essa forma de representar uma reta? Nada disso!! Temos ainda a forma paramétrica, simétrica e a reduzida. Vamos falar de cada uma ;).
Equação paramétrica da reta
A forma paramétrica é na verdade uma forma diferente de escrever a equação vetorial. Se escrevermos coordenada a coordenada a expressão vetorial da reta:
teremos as seguintes equações:
Então, essas são as equações paramétricas da nossa reta. Escrevendo de uma forma genérica, temos:

Equação simétrica da reta
As equações simétricas da reta provêm da paramétrica. Mas, como? Se isolarmos o parâmetro nas equações da nossa reta, teremos o seguinte:
E se igualarmos todas as equações, teremos:
Pronto, achamos as equações simétricas da nossa reta ;). Escrevendo ela genericamente, temos:
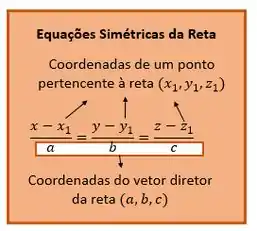
Nas Equações Simétricas vale ressaltar que como elas são uma divisão, elas só existirão se , pois não faz sentido uma divisão por zero.
Equação reduzida da reta
Bom, você, talvez, esteja pensando: A reduzida deve ser um desdobramento das Equações Simétricas!!! E é exatamente isso!
A equação reduzida consiste em escrevermos duas das coordenadas em função da terceira. Como assim? É tipo se eu escrever e em função de . Como eu faria isso usando as simétricas? Bem, por meio das simétricas, podemos escrever:
Isolando na primeira e na segunda temos:
Para a nossa reta, teríamos:
Importante: Em qualquer uma das 4 equações da reta as variáveis e representam as coordenadas de um ponto geral pertencente à reta.
Não ficou 100% ainda? Bora praticar, que você vai ficar fera!!
