Operações com Vetores
Produzido por Aline BuzziTeoria
Assim como os números os vetores pode ser somados, subtraídos e multiplicados! Bora entender como é feita as Operações com Vetores?
Soma de Vetores
Uma das principais operações que podemos realizar com vetores é a soma! Pra isso vamos considerar os seguintes vetores abaixo:
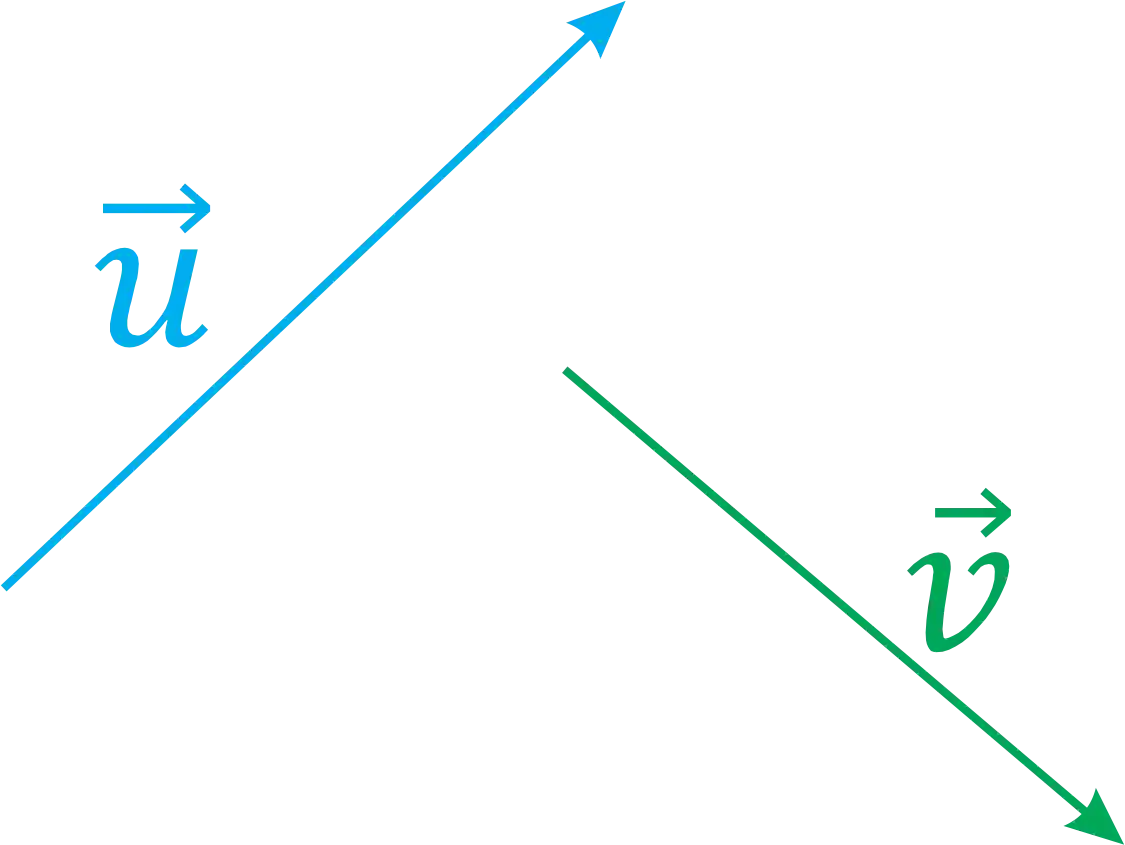
E se eu te pedisse pra somar esses vetores, como você faria?! Vou te dar uma dica…existem duas formas!
📢 Clique para ver mais:
Regra do Fechamento do Triângulo
A regra do fechamento do triângulo é bem simples! A gente coloca o início de um vetor no final do outro, assim:
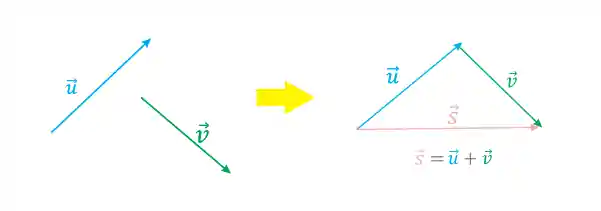
A soma dos vetores será o vetor resultante
Por exemplo, se tivermos os vetores
Regra do Paralelogramo
Quando não conseguimos colocar a extremidade de um vetor na origem do outro, usaremos a regra do paralelogramo! Se liga na figura aqui de baixo:
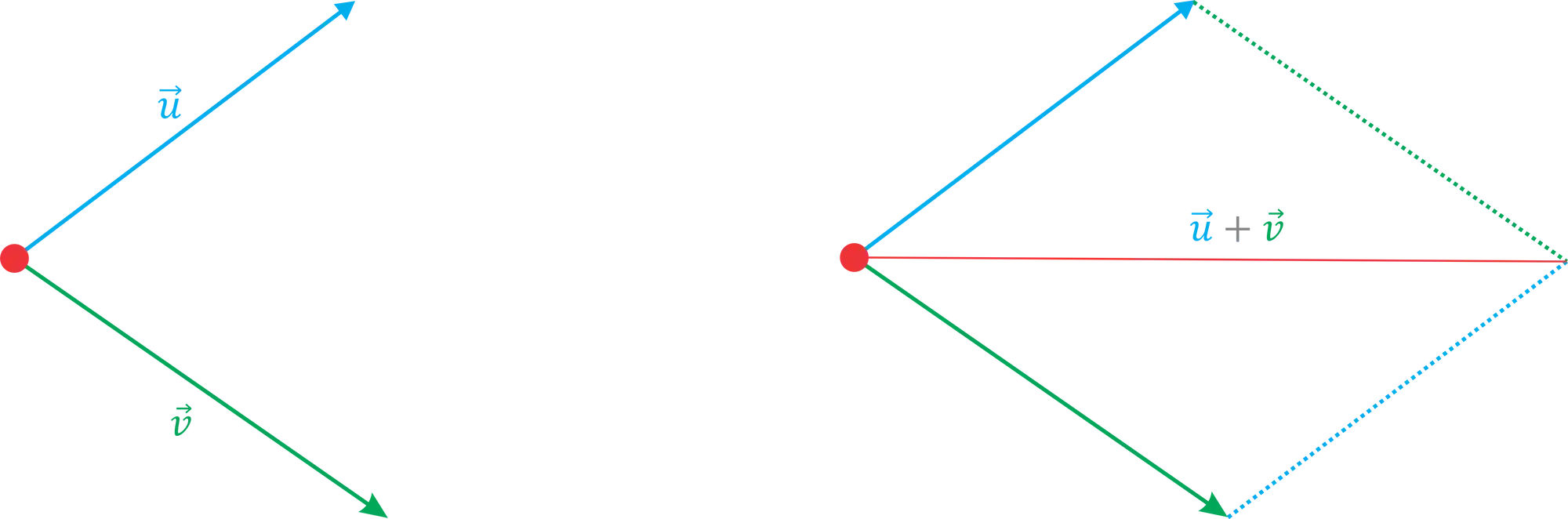
Para somar os vetores com a regra do paralelogramo, é só traçar duas retas até elas se encontrarem, formando um paralelogramo, quando isso acontecer, o vetor soma, também conhecido como resultante, será a diagonal do paralelogramo formado.
Propriedades da soma de vetores
Na soma de vetores temos as seguintes propriedades:
- Comutativa:
- Associativa:
Quer conhecer as outras operações com vetores?! Então confere esse vídeo super completo! 👇
Subtração de Vetores
Na subtração de vetores, ou diferença de vetores é uma operação bem parecida com a soma. o que muda é que na diferença usaremos vetores opostos, assim:
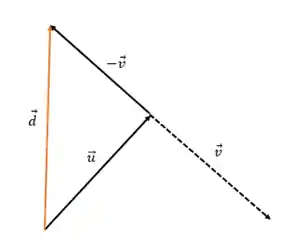
Para calcular, fazemos:
A regra do paralelogramo também funciona nesse caso:
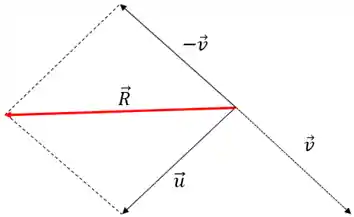
No qual
Essa operação é a soma do vetor
Decomposição de Vetores
Decompor um vetor é reescreve-lo como uma combinação linear de outros vetores. Como mostra a figura a seguir:
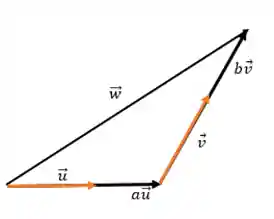
Para isso fazemos:
Multiplicação por um Número Real
E por fim, temos a multiplicação de um vetor por um número real k. Quando multiplicamos um vetor por um número real a sua direção não é alterada. Entretanto, o seu sentido e o seu módulo podem ser alterados.
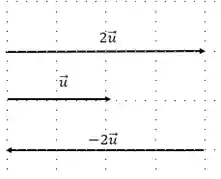
Como mostra a figura, temos o vetor
Propriedades da multiplicação por um número real
Na multiplicação por um número real, consideramos as seguintes propriedades:
Agora vamos praticar com exercícios?
Subtração de Vetores
Decomposição de Vetores
Multiplicação por um Número Real
Exercícios Resolvidos
Exercício Resolvido #1
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 3-1.
Dados os vetores e da figura, mostrar, num gráfico, um representante do vetor:
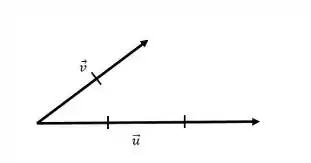
Passo 1
O exercício nos deu o desenho dos dois vetores que devemos considerar. Com esse desenho devemos realizar operações entre vetores. Aqui, como foi nos pedido devemos desenhar os vetores.
Passo 2
- Temos que achar o vetor que é
- Agora, o vetor a ser encontrado é
- Próximo vetor:
- Desenhar
Para resolver esse item, temos que lembrar que , ou seja, o vetor no sentido oposto.
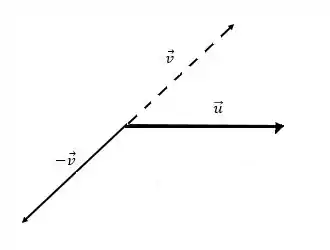
Podemos também transladar o vetor sem mudar o módulo, e sentido do vetor:
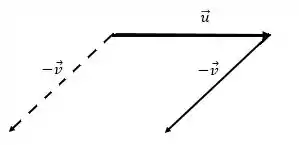
Dessa forma, podemos fazer a soma de vetores:
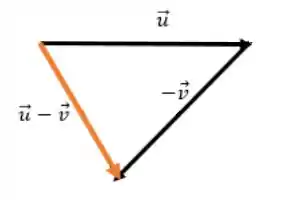
Prontinho, conseguimos o vetor , seguimos os seguintes passos:
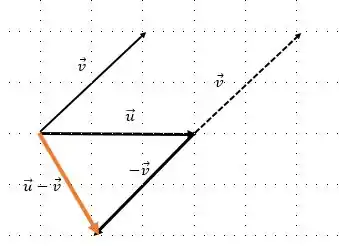
Passo 3
Da mesma forma do item (a), vamos transladar o vetor e encontrar o vetor :
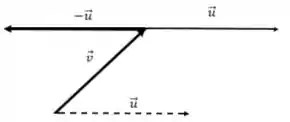
Agora podemos encontrar a soma de vetores:
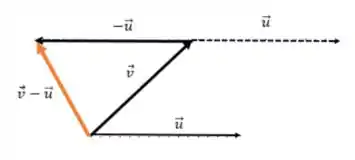
Passo 4
Primeiro vamos encontrar o vetor e :
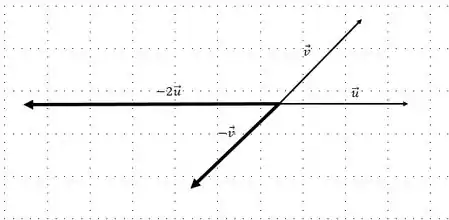
Agora podemos encontrar a soma de vetores:
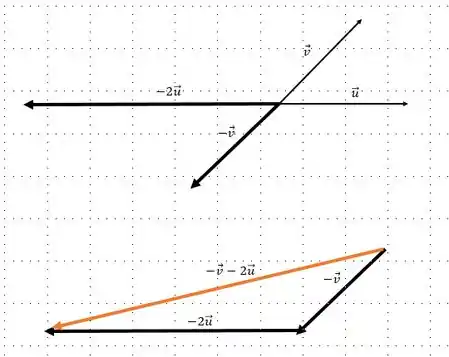
Passo 5
Até então, estávamos usando a proporção dos quadrados , mas como a figura ficaria muito grande fizemos que quadriculado equivale a .
Primeiro, vamos encontrar os vetores para soma :
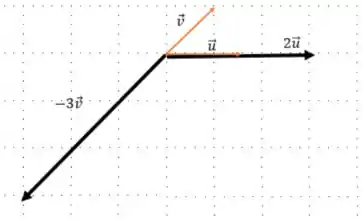
Podemos transladar o vetor para a esquerda para podermos encontrar a soma mais facilmente:
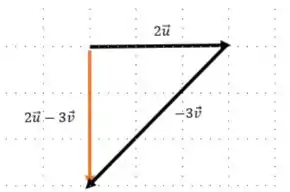
Show de bola?!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 14-3.
Sabendo que o ângulo entre os vetores e é de , determinar o ângulo formado pelos vetores:
- e
- e
- e
- e
Passo 1
O enunciado nos diz que o ângulo entre os vetores e é de . Então, temos que:
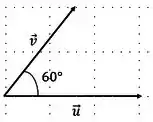
Queremos determinar,a gora, o ângulo entre diferentes vetores. Para isso, vamos utilizar o método das figuras, ou seja, vamos desenhar os vetores, para achar os ângulos.
- O primeiro ângulo, é entre os vetores e
- Próximo ângulo é entre e
- Ângulo entre os vetores e
- Ângulo entre e
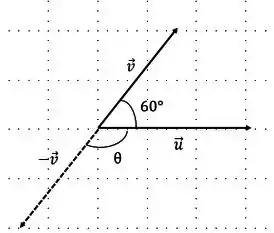
Passo 2
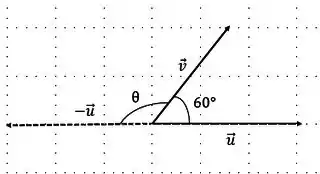
Passo 3
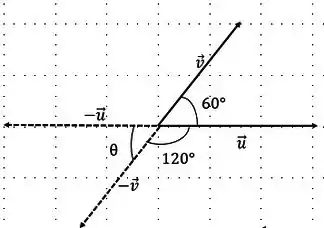
Passo 4
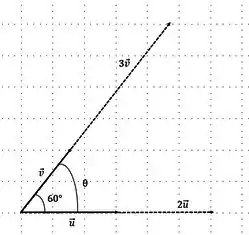
Resposta
- , b) , c) e d)
Exercício Resolvido #3
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 22-2.
Encontrar os números e tais que
, sendo e .
Passo 1
Opa!! Agora o exercício ficou um pouco diferente!! Não é preciso desenhar para conseguirmos chegar no resultado, pois os vetores são dados na base cartesiana.

Então, é só somarmos as coordenadas!!
Bom, o problema nos dá um vetor que é combinação linear, ou seja, é a soma de dois outros vetores: . Mas, ele não quer saber quem é , pois sabemos quem é . O problema quer os valores das constante , para que o vetor possa ser uma combinação linear dos outros dois vetores.
Passo 2
Então, vamos colocar na expressão os dados que o enunciado nos deu:
Essa, expressão é uma operação entre vetores. Então, vamos somar as componentes correspondentes e depois igualar, beleza?
Passo 3
Vamos lá, então!
Dá expressão acima, temos duas expressões igualando os lados com as coordenadas.
Agora, é só resolver esse sisteminha de equações, que chegamos em:
Resposta
Exercício Resolvido #4
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 37-9.
Determinar o vetor sabendo que .
Passo 1
Bom, nesse problema temos uma expressão, e nela temos o vetor que queremos descobrir.
Passo 2
Como não sabemos quem é vamos supor que ele é:
Supondo o vamos colocá-lo na expressão que nos é dada:
Pronto, se avaliarmos essa expressão é como se tivéssemos uma soma de vetores sendo igual a outra soma de vetores. Então, como estamos trabalhando com vetores, podemos fazer o mesmo que fizemos na questão anterior, somar componente a componente e depois igualar.
Passo 3
Então teremos,
Igualando os lados com as respectivas coordenadas:
Temos que:
Resposta
Exercício Resolvido #5
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 37-13.
Calcular e de modo que os pontos e sejam colineares.
Passo 1
Temos como dados 3 pontos: . Sendo que o ponto possui incógnitas nas suas coordenas e devemos determina-las. Para determinar devemos forçar os pontos a serem colineares.
Passo 2
Bom, pela teoria, sabemos que dois vetores são colineares quando estão na mesma direção, estando sobre a mesma reta ou paralelos. Vamos representar na mesma reta:
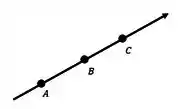
Então, como pela teoria temos que dois vetores são colineares ou paralelos se são múltiplos entre si, então temos que:
Poderíamos, ter escolhido outros vetores que o resultado não se alteraria.
Só precisamos então determinar os vetores e igualar as coordenadas.
Passo 3
Agora, só igualar:
Determinado , conseguimos descobrir .
Resposta
Exercício Resolvido #6
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 37-3.
Dados os pontos e , calcular e .
Passo 1
Nesse problema, nos é dado pontos. Precisamos determinar a diferença entre vetores.
Como vimos na teoria, quando temos as coordenadas, dadas no plano cartesiano, não precisamos ficar desenhando os vetores como fizemos nos primeiros exercícios do capítulo. Basta, calcular os vetores e para realizar a operação entre eles é só realizar coordenada a coordenada. Achou confuso? Então, vamos devagar!

Passo 2
Primeiro vamos calcular todos os vetores que vamos precisar, que são: e . Mas, pera!! Os pontos dados foram , quem é o ?

O indica a origem do plano cartesiano, vamos dizer, que é uma convenção. Assim, sempre que você ver você já sabe que é o ponto ;).
Sabendo disso, agora conseguimos calcular todos os vetores.
Vamos começar, que não são poucos hehe.
Passo 3
Pronto agora já temos todos os vetores! É só começar a encontrar os vetores pedidos. O primeiro é
O segundo é
O último

Resposta
Exercício Resolvido #7
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 24-3.
Dados os pontos e , determinar de modo que .
Passo 1
Nos é dado uma igualdade de vetores, e pontos. Sendo que os vetores dependem desses pontos. Mas, falta o ponto que é o que queremos determinar.
Dados: Pontos
O ponto é uma suposição apenas.
Passo 2
A igualdade possui dois vetores: . Mas, quem são esses vetores, suas coordenadas?
Pela teoria vimos que esses vetores são a subtração de seus pontos extremos, então temos que:
Passo 3
Agora que já temos os vetores que precisamos, é só usar a igualdade que nos foi dada.
Igualando as coordenadas correspondentes, temos:
Então,
Resposta
Exercício Resolvido #8
Elaboração própria
Sabendo que e , determine , sendo .
Passo 1
Show! O enunciado já deu para gente os vetores e , então é só substituir em
Resposta
Exercício Resolvido #9
Elaboração própria
Sabendo que e é o vetor que vai do ponto até o ponto
, determine o valor de para que
Passo 1
Bom, primeiro precisamos descobrir quem é . Felizmente, sabemos que um vetor é definido pela subtração de suas coordenadas finais (no nosso caso é o ponto ) com suas coordenadas iniciais (no nosso caso é o ponto ).
Fazendo :
Logo,
Passo 2
Agora que já descobrimos quem é , podemos usar a informação “”, dada no enunciado, para achar !
Como queremos que ,