Produto Vetorial
Produzido por Aline BuzziTeoria
Opa, seja bem vindo ao Responde Aí! Bora bater um papo sobre produto vetorial?
O que é um Produto Vetorial?
O produto vetorial é utilizado quando queremos multiplicar vetores! Se liga só:
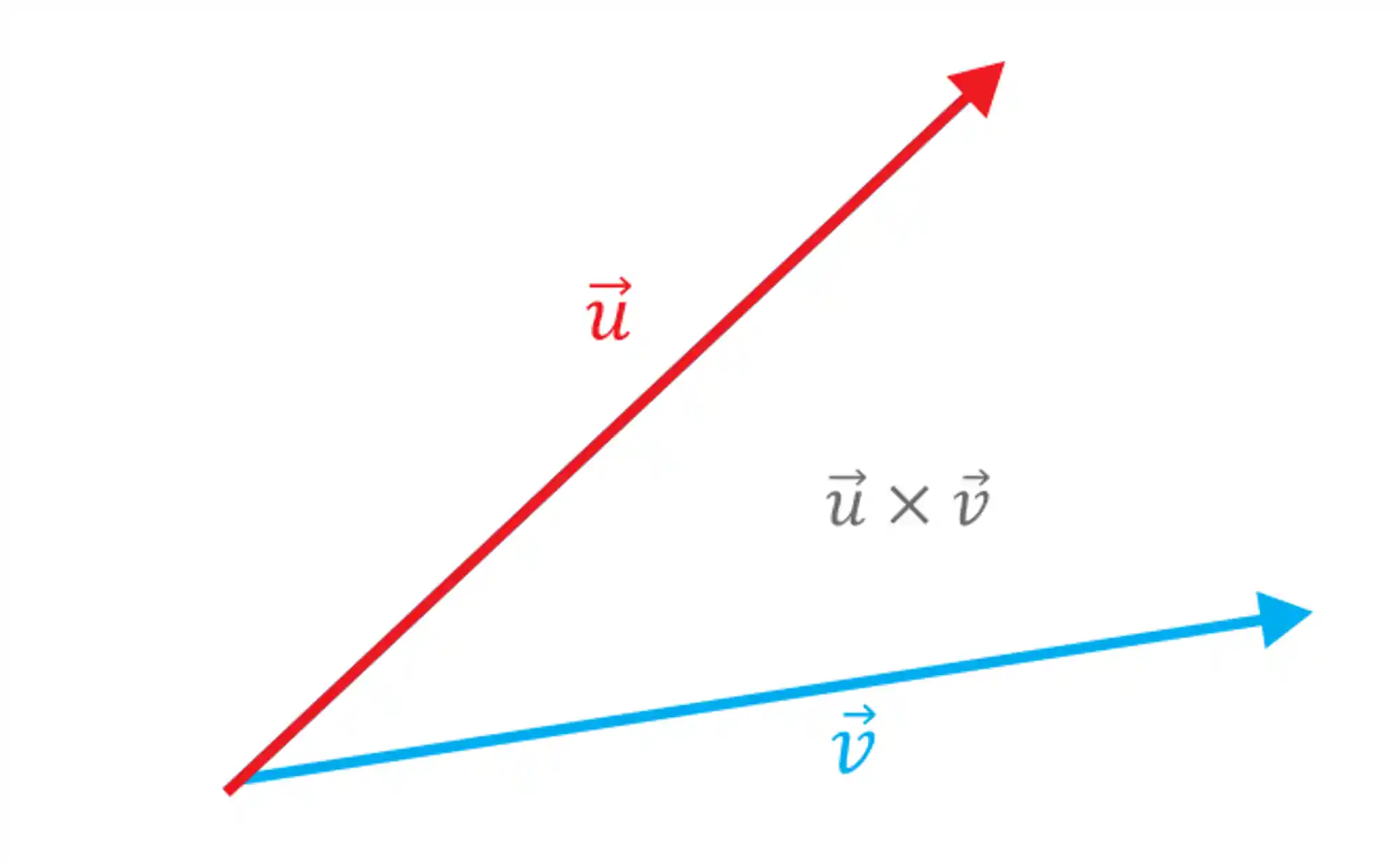
A multiplicação dos vetores
📢 Clique para ver mais:
Como Calcular o Produto Vetorial entre Dois Vetores
Vamos imaginar os seguintes vetores diretores:
Podemos escreve-los da seguinte forma:
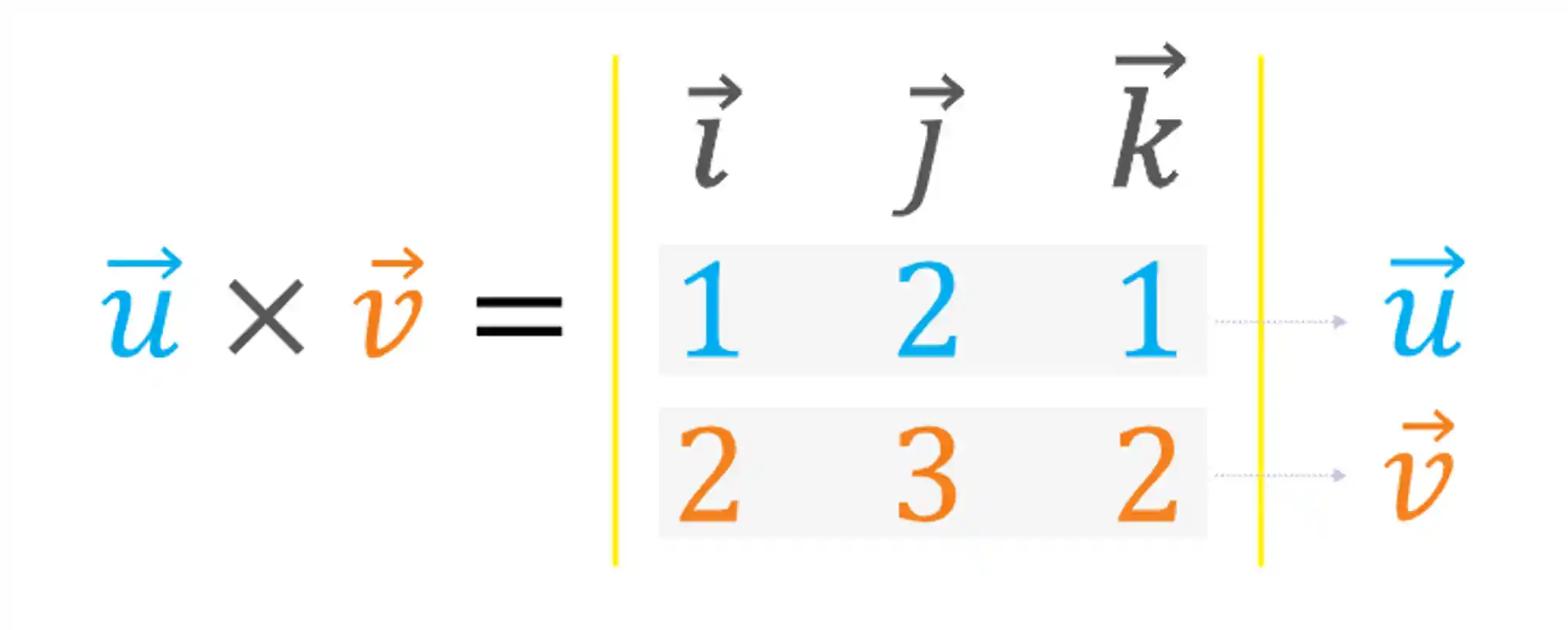
Pra calcular o produto vetorial entre esses dois vetores, só precisamos calcular o determinante:
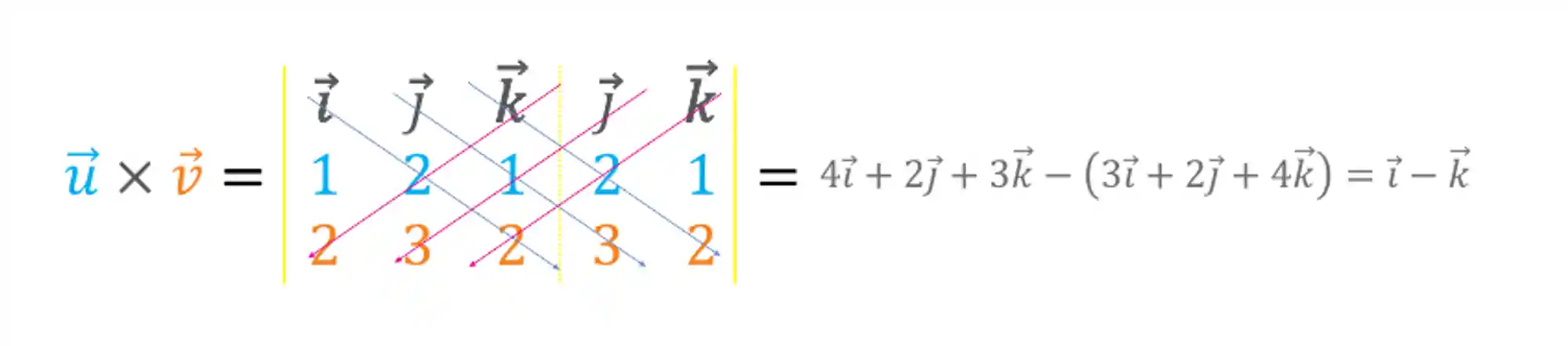
Logo o nosso produto vetorial é igual a:
Você também pode conferir esse conteúdo em vídeo:
Propriedades do Produto Vetorial
Pra finaliza vamos dar uma olhada nas propriedades do produto vetorial!
O produto vetorial entre dois vetores iguais é igual a zero
Podemos escrever que
O produto vetorial não é comutativo
Isso quer dizer que
O produto vetorial é não é Associativo
Ou seja
O produto vetorial é distributivo
Ou seja
Vetores colineares ou nulo
Podemos escrever que
Vetores ortogonais
O produto vetorial
Agora vamos praticar com exercícios?
Propriedades do Produto Vetorial
Exercícios Resolvidos
Exercício Resolvido #1
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 90-1.
Calcule sendo (referidos a uma base ortonormal positiva ).
Passo 1
Vamos aquecer os motores!!!

Bom, o problema pede para calcularmos o produto vetorial , sendo que nos é dado os vetores . Até aí eu entendi!! Mas, e o que quer dizer a frase “referidos a uma base ortonormal positiva ”?
Bem, ela só nos diz que devemos considerar a base cartesiana, é mais para reforçar mesmo, porque dificilmente trabalhamos com outras bases, só mais para frente veremos. Mas, isso vemos depois, foco aqui!
Passo 2
Agora é aplicar o que vimos na teoria, montar o determinante direitinho e depois resolvê-lo.
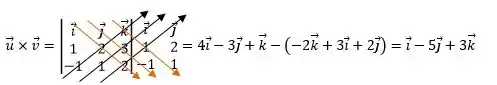
Então,
Lembrando, o produto gera um vetor.
Resposta
Exercício Resolvido #2
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 93-50.
Mostrar num gráfico um representante de cada um dos seguintes vetores:
Passo 1
São nos dados vetores na base cartesiana. E pede para que representemos num gráfico. Para cada um teremos que calcular o produto vetorial entre os vetores dados e depois desenhar num gráfico. Temos duas formas de fazer isso. Em cada item será apresentada uma forma.
Passo 2
- Primeira maneira de se resolver: Maneira analítica
No item nos é dado . Pode parecer uma representação esquisita, mas ela está na base cartesiana, ou seja:
- indica a coordenada .
- indica a coordenada .
- indica a coordenada
Assim, é nos dado o seguinte produto vetorial:
Agora que sabemos a representação mais comum a nós, vamos fazer o produto vetorial:
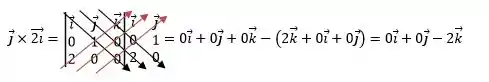
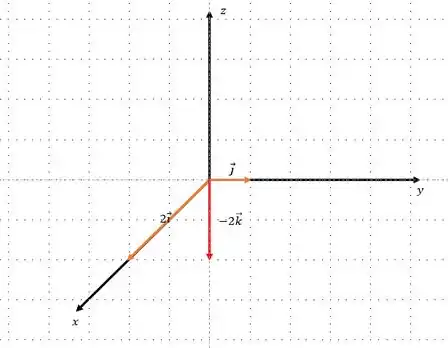
Passo 3
Agora que já sabemos interpretar a representação cartesiana, fica mais tranquilo identificarmos os vetores .
Se dominamos a regra da mão direita e a base cartesiana, esse jeito pode ser mais rápido.
Bom, primeiro, sabemos que os versores da base cartesiana são ortogonais entre si, então, pela regra da mão direita sabemos que:
A direção e o sentido do nosso produto vetorial nós já achamos, simplemente aplicando a regra da mão direita. Mas, qual o módulo?
Bom, sabemos que:
Como sabemos, o Ângulo entre e é , assim temos que:
Então,
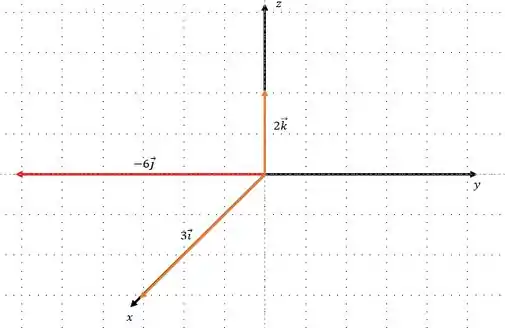
Resposta
Exercício Resolvido #3
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 73-18.
Dados os vetores , calcular a área do paralelogramo determinado pelos vetores .
Passo 1
O enunciado nos pede para clacular a área do paralelogramo formado pelos vetores . Sabemos da teoria que a área é o módulo do produto vetorial .
Passo 2
Então, vamos calcular o produto vetorial primeiro e depois fazemos o módulo do vetor encontrado. Para isso vamos determinar os vetores .
Agora é montar o determinante!

Passo 3
Como queremos a área é só calcular o módulo do vetor encontrado.
Então,

Resposta
Exercício Resolvido #4
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 74-19.
Sejam os vetores . Calcular o valor de para que a área do paralelogramo determinado por seja igual a .
Passo 1
O enunciado nos pede o valor de para que o paralelogramo formado por tenha área de .
Como eu acho o ?

Bem, nós sabemos que a área do paralelogramo formado pelos vetores é . Sabemos pela teoria que o módulo do produto vetorial é a área do paralelogramo. Então, fazemos o produto vetorial e depois calculamos o módulo para achar ;).
Passo 2
Então, vamos calcular primeiro o produto vetorial:
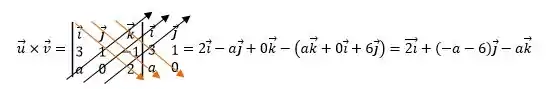
Passo 3
Temos o vetor resultante do produto vetorial, então agora é só calcularmos o módulo:
Resolvendo a equação de 2º grau, chaga-se em:
Resposta
Exercício Resolvido #5
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 94-51.
Sabendo que e é o ângulo entre e , calcular .
Passo 1
O enunciado nos dá os seguintes dados:
E nos pede para calcular
Passo 2
Bem, vamos pensar!!! Esses dados não te fazem lembrar de uma relação que vimos lá na teoria?

Tudo bem!!! Vamos relembrar ;).
Olha essa relação:
Uau!! Parece que nosso problema está resolvido uhuuuu...é só colocar na fórmula os dados e sair para o abraço .
Resposta
Exercício Resolvido #6
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 93-47.
Determinar o valor de para que o vetor seja simultaneamente ortogonal aos vetores e .
Passo 1
O problema nos fornece os seguintes dados:
Dados:
Com esses dados, o exercício pede para determinarmos o valor de para que o vetor seja ortogonal (forme ) simultaneamente aos vetores e .
Buguei na parte que fala “simultaneamente ortogonal”!!!

Vamos relembrar um detalhe que vai nos ajudar ;).
Passo 2
Na teoria vimos algumas propriedades do produto vetorial! Lembra? Pois é, eu sei que eram muitos, mas uma delas vai nos ajudar muito. Essa aqui!
![]()
Matou a charada?
Então, sabemos que o produto vetorial gera um vetor, e ainda a propriedade nos diz que esse vetor é simultaneamente ortogonal aos dois vetores que o formam. É tudo o que precisamos. Então, para acharmos , precisamos forçar que ou também que , no caso iremos obter vetores oposto.
Passo 3
Então agora é mão na massa!!!
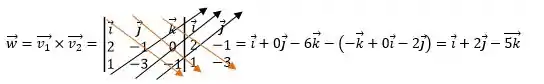
Se você fizer , chegarás em:
Nesse caso, a conta só vai fazer sentido com , pois em e igualando a , teremos:
Resposta
Exercício Resolvido #7
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 93-49.
Determinar um vetor unitário simultaneamente ortogonal aos vetores e . Nas mesmas condições, determine um vetor de módulo 5.
Passo 1
O problema nos dá dois vetores e . Com esses dois vetores devemos determinar um vetor que seja ortogonal aos dois vetores dados e além disso, que seja unitário.
Bom, no exercício anterior vimos que se realizarmos o produto vetorial entre e , o vetor resultante será ortogonal a esses dois vetores. Okay, essa parte já entendemos!! E o unitário onde entra nessa história?

Calma!! Você vai entender tudinho!!
Na teoria não chegamos a falar sobre o termo “unitário”, mas ele significa que o módulo do vetor deve ser unitário. Assim, esse vetor é chamado de “versor”. Para achar o vetor unitário basta calcular o seu módulo e dividir cada coordenada pelo seu módulo, assim oh:
Passo 2
Agora, é fazermos as conta. Vamos começar resolvendo o produto vetorial :
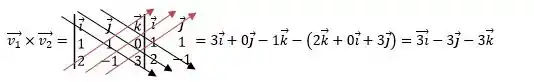
Achamos o vetor que queríamos, que é . Agora falta transformá-lo em unitário.
Passo 3
Então, para fazê-lo ter módulo unitário, vamos calcular primeiro o seu módulo, que é:
O vetor unitário que estamos procurando será:
É bom lembrar que se considerarmos , obteremos como resultado o oposto do vetor obtido anteriormente, pois:
Passo 4
Já temos o vetor unitário, agora queremos calcular um vetor de módulo cinco nas mesmas condições do anterior. Se nas mesmas condições do anterior podemos utilizar o resultado que temos.
Vamos pensar um pouco... Se o vetor que encontramos é unitário, ou seja, seu módulo é unitário, então, isso significa que se multiplicarmos as suas coordenadas por , o vetor passará a ter módulo ?

É exatamente isso. Então, o vetor de módulo é:
Resposta
Exercício Resolvido #8
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 75-20.
Calcular a área do triângulo de vértices
Passo 1
Temos os vértices de um triângulo que são os pontos . Com esses pontos devemos determinar a área do triângulo.
Na teoria vimos como calcular a área de um paralelogramo, então sucesso, já sabemos como fazer. Opa! Mas, aqui é a aréa de um triângulo!!! Como faremos?

Ahh precisamos de uma informação valiosa lá do colégio. Quando aprendemos que a área de um paralelogramo é duas vezes a área de um triângulo. Então, temos que:
Passo 2
Então, a área do paralelogramo sabemos calcular!
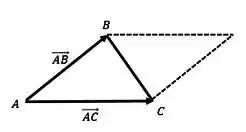
Pela figura, temos os vértices do triângulo . Para calcular a área do paralelogramo formado pelos vetores , sabemos pela teoria que equivale ao módulo do produto vetorial entre esses dois vetores:
Então, primeiro precisamos calcular o produto vetorial. Mas, antes precisamos calcular os vetores , pois foi nos dado os pontos apenas.
Agora sim, podemos calcular o produto vetorial:
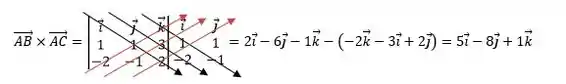
Passo 3
Agora que temos o produto vetorial, vamos calcular o módulo do vetor, para encontrar a área do paralelogramo.
Passo 4
Mas, não é ainda o que queremos. Queremos a área do triângulo que como falamos antes é:
Então, temos que . Assim:
Depois de fazermos as contas, vamos fazer um questionamento: E se, tivéssemos utilizado, outros vetores, como, por exemplo, alteraria nosso resultado?
O resultado deve ser o mesmo, pois o resultado final é dado em módulo, e esse é igual para qualquer vetor considerado.
Resposta
Exercício Resolvido #9
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 94-59.
Calcular , sabendo que são vértices de um triângulo de área .
Passo 1
Esse exercício é meio que o inverso do anterior, pois é nos dado os pontos que formam o triângulo e também é nos dada a área do triângulo. Então, o que devemos descobrir é a coordenada do ponto para que o triângulo tenha área .
Sabemos que o módulo do produto vetorial entre os vetores nos dará a área do paralelogramo, e que a área do paralelogramo é duas vezes a do triangulo, então temos que:
Passo 2
Sabendo a área do paralelogramo, sabemos quanto deve dar o módulo do produto vetorial entre . Então, vamos calcular o produto vetorial, mas primeiro vamos achar os vetores que precisamos.
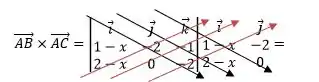
Passo 3
Já temos o produto vetorial. Agora, é calcular o módulo e igualar com a área do paralelogramo que já descobrimos quanto vale:
Resolvendo a igualdade acima, temos:
Resolvendo a equação de 2º grau chegamos em duas soluções:
Resposta
Exercício Resolvido #10
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 98-20.
Prove que se e então ou . Interprete geometricamente.
Passo 1
Esse exercício requer conhecimentos do produto escalar e do produto vetorial. Bem, o enunciado pede para provarmos que se dizemos que os vetores e então ou .
Passo 2
Vamos, analisar cada parte, começando por . Do produto escalar temos que:
Se o enunciado nos diz que , então pela expressão acima temos três possibilidades:
- O ângulo entre os vetores , ou seja, .
- O ângulo entre os vetores , ou seja, .
Analisando a segunda afirmação e a relação do produto vetorial, temos :
Passo 3
Já temos tudo o que podemos concluir com os dados que nos foram dados. Agora como sabemos que a relação entre e é de E, ou seja, é de intersecção, então, concluimos que:
c.q.d
Falta falarmos da interpretação geométrica do problema. Bom, pensando geometricamente, sabemos que esses vetores não são paralelos entre si e nem formam . Então, poderiam formar qualquer ângulo diferente de . Mas, para satisfazer as duas condições do produto escalar e vetorial, a única possibilidade é a de que um dos vetores seja nulo.
Resposta
Ei, a resposta está no passo a passo :)