Esboce o diagrama de Bode para a função de transferência de um sistema em malha aberta mostrada abaixo e determine sua estabilidade em malha fechada.
Passo 1
Antes de determinar a estabilidade do sistema, precisamos esboçar o diagrama de Bode do sistema.
Vamos esboçar cada um dos termos como uma linha no diagrama de Bode:
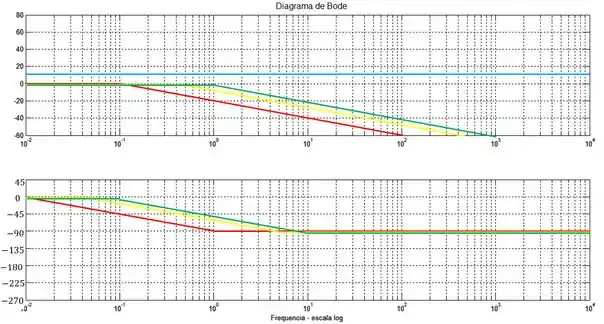
A linha azul representa a constante e as linhas vermelha, amarela e verde representam os polos com frequência de quebra em , e respectivamente
Se você não lembra as regras para traçar um esboço do diagrama de Bode através da aproximação por assíntotas, seria bacana dar uma revisadinha na aula de Diagrama de Bode.
Passo 2
Somando todas as assíntotas, teremos:
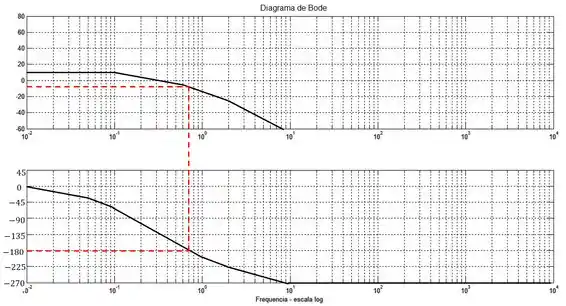
Para determinar a estabilidade precisamos encontrar a frequência em que o ângulo de fase é igual a e rebater para cima para encontrar a razão de amplitude nessa frequência.
Passo 3
Sendo assim, já temos tudo que precisamos para determinar a estabilidade do sistema.
O critério de Bode diz que para um certo sistema ser estável, em malha fechada, a sua função de transferência, em malha aberta, deve ter razão de amplitude menor que na frequência crítica, que é a mesma frequência em que o ângulo de fase é igual a . Ou seja, em decibéis, a razão de amplitude precisa ser menor que , já que:
Podemos ver que na frequência crítica, a razão de amplitude, em decibéis, é negativa para o sistema do enunciado, portanto, o sistema é estável.
Resposta
Sistema estável