Esboce o diagrama de Bode para a função de transferência de um sistema em malha aberta mostrada abaixo e determine sua estabilidade em malha fechada.
Passo 1
Antes de determinar a estabilidade do sistema, precisamos esboçar o diagrama de Bode do sistema. O sistema é composto por uma conntante (o ganho) , um polo na origem e um polo em de segunda ordem.
Vamos esboçar cada um dos termos como uma linha no diagrama de Bode:
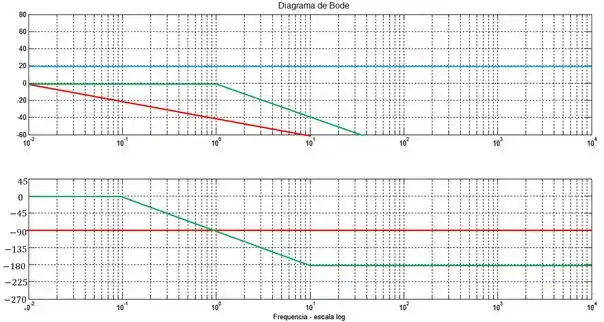
A linha azul representa a constante , a linha vermelha é o polo na origem e a linha verde o polo em .
Se você não lembra as regras para traçar um esboço do diagrama de Bode através da aproximação por assíntotas, seria bacana dar uma revisadinha na aula de Diagrama de Bode.
Passo 2
Somando todas as assíntotas, teremos:
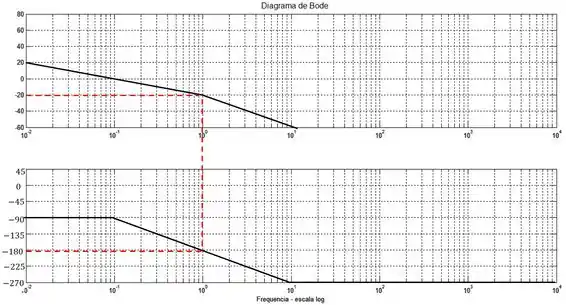
Para determinar a estabilidade precisamos encontrar a frequência em que o ângulo de fase é igual a e rebater para cima para encontrar a razão de amplitude nessa frequência.
Passo 3
Sendo assim, já temos tudo que precisamos para determinar a estabilidade do sistema.
O critério de Bode diz que para um certo sistema ser estável, em malha fechada, a sua função de transferência, em malha aberta, deve ter razão de amplitude menor que na frequência crítica, que é a mesma frequência em que o ângulo de fase é igual a . Ou seja, em decibéis, a razão de amplitude precisa ser menor que , já que:
Podemos ver que na frequência crítica, a razão de amplitude, em decibéis, é aproximadamente , portanto, o sistema é estável.
Resposta
Sistema estável