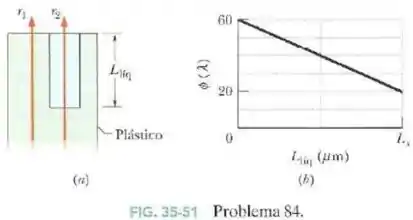
A Fig.35-51a mostra dois raios luminosos, com um comprimento de onda no ar de , que estão inicialmente em fase enquanto se propagam para cima em um bloco de plástico.
O raio atravessa o plástico e chega ao ar. Antes de chegar ao ar o raio passa por um líquido contido em uma cavidade do plástico. A altura do líquido é inicialmente , mas o líquido começa a evaporar.
Seja a diferença de fase entre os raios e ao chegarem ao ar. A Fig.35-51b mostra o valor de (em comprimentos de onda) em função da altura do líquido, com dado em termos de comprimentos de onda e a escala do eixo horizontal definida por . Determine:
- O índice de refração do plástico.
- O índice de refração do líquido.
Passo 1
Primeiro, vamos entender o problema.
Os dois raios luminosos se propagam, inicialmente, no mesmo meio (o plástico) e em fase até que o raio atinge a cavidade com líquido.
Assim, a diferença de fase entre eles na saída será devido a diferença de meio de propagação.
Contudo, é importante notar que, inicialmente, essa diferença de meio se dá apenas pelo líquido, mas a medida que o líquido evapora ela vai se dando pelo líquido e pelo ar na cavidade.
Passo 2
a)
A diferença de fase dada pela diferença de meio de propagação em múltiplos do comprimento de onda é dada por:
Pelo gráfico, temos diversos valores de para diversos valores de , e a altura de ar vai ser a altura da cavidade menos a altura do líquido. O problema também nos dá o comprimento de onda da luz incidente.
Para inverter a equação, e achar um dos dois índices de refração, é necessário ter o outro índice.
Tem um meio cujo índice de refração sabemos, mesmo sem o problema nos contar: o ar, cujo índice de refração é 1.
Passo 3
A medida que o líquido evapora, a cavidade vai ficando com ar dentro dela. Quando o líquido evaporar completamente () teremos apenas ar na cavidade que tem uma altura de (altura inicial do líquido). Temos então:
- (obtido na letra (a) )
Passo 4
b)
Para encontrar o índice de refração do líquido, podemos “inverter o tempo”. No início do processo, a cavidade tinha apenas o líquido (antes de ele evaporar). Com isso, podemos usar uma equação semelhante a anterior para achar o índice de refração do líquido usando o índice do plástico.
Passo 4
Os valores da equação nós já temos. Lembrando que a diferença de fase nós tiramos do gráfico (neste caso, usamos , o extremo direito do gráfico )
Resposta
a)
b)