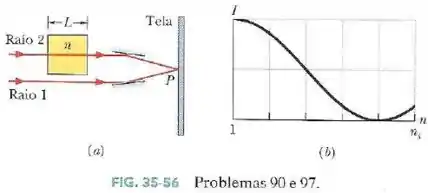
Na Fig.35-56a, as ondas associadas aos raios e estão inicialmente em fase e têm o mesmo comprimento de onda no ar. O raio atravessa um material de comprimento e índice de refração .
Os raios são em seguida refletidos por espelhos para um ponto comum , situado sobre uma tela. Suponha que é possível fazer variar de até . Suponha também que de a a intensidade da luz no ponto varia com da forma indicada na Fig.35-56b.
Para que valores de maiores que a intensidade :
- É máxima?
- É zero?
- Que múltiplo de corresponde à diferença de fase entre os raios no ponto para ?
Passo 1
a)
Quando a interferência é totalmente construtiva a intensidade é máxima, e quando é totalmente destrutiva a intensidade é mínima.
As condições para isso quando temos uma diferença de fase por meio de propagação são:
Interferência construtiva:
Interferência destrutiva:
Lembrando que o raio está sempre no ar, temos que (o índice de refração do ar é aproximadamente 1).
Passo 2
Para sabermos quando que a interferência será construtiva ao variarmos precisamos encontrar a razão .
Pelo gráfico de intensidade, sabemos que é o primeiro índice de refração acima de 1 que causa interferência destrutiva. Logo, para este valor, .
Passo 3
Agora, para acharmos os valores de com interferência construtiva (intensidade máxima), vamos variando até passarmos de (evitamos pois ele corresponde a ). Rearranjando a condição:
Onde e .
E paramos por aqui, pois .
Passo 4
b)
A intensidade zera para o caso de interferência totalmente destrutiva. Manipulando um pouco a condição de interferência destrutiva:
Como tínhamos calculado no item anterior, e . Novamente, vamos testando diversos valores de depois do 0 até ultrapassarmos o limite de índices de refração possíveis.
Para , e por isso paramos por aqui.
Passo 5
c)
A diferença de fase em múltiplos do comprimento de onda é dada por:
Dos itens anteriores, sabemos que e por isso .
Resposta
a)
A intensidade é máxima para .
b)
A intensidade é zero para .
c)
A diferença de fase dos raios no ponto para é de comprimentos de onda.