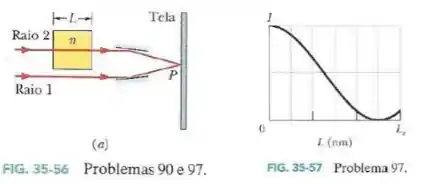
Na Fig.35-56a, as ondas associadas aos raios e estão inicialmente em fase e têm o mesmo comprimento de onda no ar. O raio atravessa um material de comprimento e índice de refração . Os raios são refletidos por espelhos para um ponto comum , situado sobre uma tela.
Suponha que seja possível fazer variar de até . Suponha também que de até a intensidade da luz no ponto varia com da forma indicada na Fig.35-57.
Para que valores de maiores que a intensidade :
- É máxima?
- É zero?
- Que múltiplo de corresponde à diferença de fase entre os raios no ponto para ?
Passo 1
Existem mais de uma forma de resolver um mesmo exercício.
Primeiro, podemos resolver esse exercício de forma metódica: usamos as condições de interferência construtiva e destrutiva junto com o gráfico de intensidade em função de para encontrar os valores necessários para o problema.
Mas existe uma outra forma de resolver também, que é usando as oscilações do gráfico de intensidade. Vamos seguir por esse caminho.
Passo 2
a)
A intensidade da onda resultante da interferência de duas ondas eletromagnéticas depende do cosseno da diferença de fase entre as duas.
Onde a diferença de fases é dada por
Note que depende diretamente da espessura do meio 2.
Sabemos então que o gráfico da intensidade contra vai se repetindo sempre!
Passo 3
Se o gráfico se repete, então a distância entre o primeiro máximo e o primeiro mínimo de intensidade e a distância entre o primeiro mínimo e o segundo máximo de intensidade serão iguais.
Como o “primeiro máximo” é dado pra , essa distância é de (pelo gráfico).
Logo, o segundo máximo está em .
Se a gente repetir essa ideia pra máximos adjacentes subsequentes, veríamos que os máximos do segundo em diante correspondem a:
Onde corresponde ao nosso segundo máximo.
Passo 4
b)
Repetiremos a mesma ideia do item anterior. O primeiro mínimo corresponde a . A distância até o segundo mínimo é a distância até o segundo máximo (), e desse até o segundo mínimo ().
O segundo mínimo então está em .
Para outros máximos, nós somamos mais e depois mais e mais e mais...
Onde corresponde ao nosso segundo mínimo.
Passo 5
c)
Na letra (a), encontramos que o primeiro máximo após é dado por .
Como o máximo é quando temos uma diferença de fase como um múltiplo inteiro do comprimento de onda, e como esse é o primeiro, podemos dizer que neste caso a diferença de fase corresponde a 1 comprimento de onda.
A quantos comprimentos de onda a diferença de fase para corresponde pode ser achado por uma regra de 3 (podemos usar isso pois ela é linear com ).
Resposta
a)
A intensidade é máxima para .
b)
A intensidade é zero para .
c)
A diferença de fase dos raios no ponto para é de comprimentos de onda.