Desenvolvendo-se o binômio , podemos dizer que a soma de seus coeficientes é:
Passo 1
Olááá, queridx alunx! Tudo bom?
Nesse exercício, nós precisamos saber a soma dos coeficientes daquele binômio. Podemos descobrir de três formas: calculando , usando o Triângulo de Pascal ou desenvolvendo o binômio.
forma (calculando ):
Sabemos que dado um polinômio , a soma dos coeficientes é :
Bem rápido, né?!
forma (Triângulo de Pascal):
Um binômio da forma tem termos.
No nosso caso, . Eu gosto de fazer da seguinte forma: como eu sei que tem termos, eu começo assim:
Mas como elevado a qualquer coisa é :
Pronto, tenho seis termos. Agora eu preencho todas as potências de , já que ele vem primeiro no binômio. As potências começam no expoente máximo, que é e vão até o :
Cara, perceba que os coeficientes vão ser justamente os caras da linha no Triângulo de Pascal.
Passo 2
Só faltam os coeficientes! E como temos termos, é tranquilo olhar no Triângulo Pascal a sexta linha!
“Ah, mas eu não sei como é o Triângulo de Pascal!”
Vou te ensinar a construir. Primeiro, você começa com o número :
Essa é a primeira linha. Lembre-se: a linha tem termos.
Vamos para a segunda linha, sabendo que o primeiro e o último termo de cada linha é o número :
![]()
E agora, a gente constrói os termos! Dessa forma:
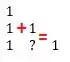
Então:

Bom, já temos linhas, olha a quarta:

Perceba que:
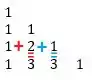
Como deveria ser! A quinta linha:

Finalmente, a sexta linha:
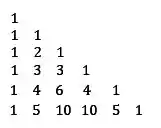
Pronto! Esses termos da linha são os nossos coeficientes. E como queremos a soma, basta soma-los:
Passo 3
forma (fórmula):
Sabendo que o um binômio da forma tem termos, a fórmula do termo geral é
No nosso caso, e . Então vamos calcular termo a termo (lembrando que temos ):
Então, temos os seguintes termos:
Então a expansão é:
Como queremos a soma dos coeficientes, temos que somar esses números binomiais!
Passo 4
Agora vamos resolver os números binomiais:
Começando:
Lembrando que .
Passo 5
Pronto! Agora substituímos:
E a soma desses termos é .