Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Binômio de Newton

Ver Teoria
Exercício 1234567

Enunciado

Desenvolver as potências abaixo:

a   x + 3 4

b   2 x - y 5

Passo 1

FAAAALA AÍ, meu anjo! Tudo bom? Vamos finalmente colocar a mão na massa! Começando do começo:

a   x + 3 4

Bom, vou fazer esse item de duas formas: usando a fórmula geral e usando o Triângulo de Pascal (jeito que eu faço). Aí você vê com qual você se identifica mais.

1 ª forma (jeito que eu faço):

Um binômio da forma a + b n tem n + 1 termos.

No nosso caso, n = 4 ,   a = x   e   b = 3 . Eu gosto de fazer da seguinte forma: como eu sei que tem 5 termos, eu começo assim:

        _ x ? 3 ? +         _ x ? 3 ? +         _ x ? 3 ? +         _ x ? 3 ? +         _ x ? 3 ?

Pronto, tenho cinco termos. Agora eu preencho todas as potências de x , já que ele vem primeiro no binômio. As potências começam no expoente máximo, que é 4 e vão até o 0 :

        _ x 4 3 ? +         _ x 3 3 ? +         _ x 2 3 ? +         _ x 1 3 ? +         _ x 0 3 ?

Agora eu preencho o expoente de 3 , a ideia é a seguinte: o expoente é o número que falta para a soma dos expoentes chegarem a 4 . Por exemplo, no primeiro termo temos o expoente 4 , para chegar a 4 falta 0 , então:

        _ x 4 3 0 +         _ x 3 3 1 +         _ x 2 3 2 +         _ x 1 3 3 +         _ x 0 3 4

Perceba que se somarmos o expoente dos dois, a soma dá 4 ,e então está tudo certinho!

Passo 2

Só faltam os coeficientes! E como temos 5 termos, é tranquilo olhar no Triângulo Pascal a quinta linha!

“Ah, mas eu não sei como é o Triângulo de Pascal!”

Vou te ensinar a construir. Primeiro, você começa com o número 1 :

1

Essa é a primeira linha. Lembre-se: a linha n tem n termos.

Vamos para a segunda linha, sabendo que o primeiro e o último termo de cada linha são o número 1 :

E agora, a gente constrói os termos! Dessa forma:

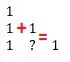
Então:

Bom, já temos 3 linhas, olha a quarta:

Perceba que:

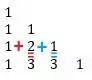
Como deveria ser! Finalmente, a quinta linha:

Passo 3

Prontinho! Vamos substituir:

        _ x 4 3 0 +         _ x 3 3 1 +         _ x 2 3 2 +         _ x 1 3 3 +         _ x 0 3 4

x 4 3 0 + 4 x 3 3 1 + 6 x 2 3 2 + 4 x 1 3 3 + x 0 3 4

E agora é só ajeitar as potências, sabendo que m 0 = 1 :

x 4 + 12 x 3 + 54 x 2 + 108 x + 81

Esse método não costuma ser longo, eu só quis esmiuçar bem para você entender o raciocínio!

Passo 4

2 ª forma (fórmula):

Sabendo que o um binômio da forma a + b n tem n + 1 termos, a fórmula do termo geral é

T k + 1 = n k a n - k b k

No nosso caso, n = 4 ,   a = x   e   b = 3 e 0 ≤ k ≤ n . Então vamos calcular termo a termo (lembrando que temos 5 ):

k = 0 → T 1 = 4 0 x 4 - 0 3 0

k = 1 → T 2 = 4 1 x 4 - 1 3 1

k = 2 → T 3 = 4 2 x 4 - 2 3 2

k = 3 → T 4 = 4 3 x 4 - 3 3 3

k = 4 → T 5 = 4 4 x 4 - 4 3 4

Então, temos os seguintes termos:

T 1 = 4 0 x 4

T 2 = 4 1 x 3 3

T 3 = 4 2 x 2 9

T 4 = 4 3 x 27

T 5 = 4 4 81

Passo 5

Agora vamos resolver os números binomiais:

n k = n ! k ! n - k !

Começando:

4 0 = 4 ! 0 ! 4 - 0 ! = 4 ! 4 ! = 1

Lembrando que 0 ! = 1 .

4 1 = 4 ! 1 ! 4 - 1 ! = 4 ! 3 ! = 4

4 2 = 4 ! 2 ! 4 - 2 ! = 4 ! 2 ! 2 ! = 4.3 2 ! = 6

4 3 = 4 ! 3 ! 4 - 3 ! = 4 ! 3 ! = 4

4 4 = 4 ! 4 ! 4 - 4 ! = 4 ! 4 ! = 1

Passo 6

Pronto! Agora substituímos:

T 1 = x 4

T 2 = 4 . x 3 3

T 3 = 6 . x 2 9

T 4 = 4 . x 27

T 5 = 81

Finalmente:

T 1 = x 4

T 2 = 12 x 3

T 3 = 54 x 2

T 4 = 108 x

T 5 = 81

Finalizando:

x 4 + 12 x 3 + 54 x 2 + 108 x + 81

Passo 7

a   2 x - y 5

Bom, vou fazer esse item de duas formas: usando a fórmula geral e usando o Triângulo de Pascal (jeito que eu faço). Aí você vê com qual você se identifica mais.

1 ª forma (jeito que eu faço):

Um binômio da forma a + b n tem n + 1 termos.

“Mas aqui nós temos um - , não um + ”

Eu sei, mas olha só o que podemos fazer: 2 x - y = 2 x + - y

No nosso caso, n = 5 ,   a = 2 x   e   b = - y . Eu gosto de fazer da seguinte forma: como eu sei que tem 6 termos, eu começo assim:

        _ ( 2 x ) ? ( - y ) ? +         _ ( 2 x ) ? ( - y ) ? +         _ ( 2 x ) ? ( - y ) ? +         _ ( 2 x ) ? ( - y ) ? +         _ ( 2 x ) ? ( - y ) ? +         _ ( 2 x ) ? ( - y ) ?

Pronto, temos seis termos. Agora eu preencho todas as potências de ( 2 x ) , já que ele vem primeiro no binômio. As potências começam no expoente máximo, que é 5 e vão até o 0 :

        _ ( 2 x ) 5 ( - y ) ? +         _ ( 2 x ) 4 ( - y ) ? +         _ ( 2 x ) 3 ( - y ) ? +         _ ( 2 x ) 2 ( - y ) ? +         _ ( 2 x ) 1 ( - y ) ? +         _ ( 2 x ) 0 ( - y ) ?

Agora eu preencho o expoente de ( - y ) , a ideia é a seguinte: o expoente é o número que falta para a soma dos expoentes chegarem a 5 . Por exemplo, no primeiro termo temos o expoente 5 , para chegar a 5 falta 0 , então:

        _ ( 2 x ) 5 ( - y ) 0 +         _ ( 2 x ) 4 ( - y ) 1 +         _ ( 2 x ) 3 ( - y ) 2 +         _ ( 2 x ) 2 ( - y ) 3 +         _ ( 2 x ) 1 ( - y ) 4 +         _ ( 2 x ) 0 ( - y ) 5

Perceba que se somarmos o expoente dos dois, a soma dá 5 ,e então está tudo certinho!

Passo 8

Só faltam os coeficientes! E como temos 6 termos, vamos olhar no Triângulo Pascal a sexta linha!

“Ah, mas eu não sei como é o Triângulo de Pascal!”

Bom, já construímos até a linha 5 :

Vamos fazer a linha 6 :

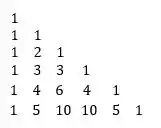
Passo 9

Prontinho! Vamos substituir:

        _ ( 2 x ) 5 ( - y ) 0 +         _ ( 2 x ) 4 ( - y ) 1 +         _ ( 2 x ) 3 ( - y ) 2 +         _ ( 2 x ) 2 ( - y ) 3 +         _ ( 2 x ) 1 ( - y ) 4 +         _ ( 2 x ) 0 ( - y ) 5

( 2 x ) 5 ( - y ) 0 + 5 ( 2 x ) 4 ( - y ) 1 + 10 ( 2 x ) 3 ( - y ) 2 + 10 ( 2 x ) 2 ( - y ) 3 + 5 ( 2 x ) 1 ( - y ) 4 + ( 2 x ) 0 ( - y ) 5

E agora é só ajeitar as potências, sabendo que m 0 = 1 e - m e x p o e n t e   p a r = m e x p o e n t e   p a r :

32 x 5 - 80 x 4 y + 80 x 3 y 2 - 40 x 2 y 3 + 10 x y 4 - y 5

Passo 10

2 ª forma (fórmula):

Sabendo que o um binômio da forma a - b n tem n + 1 termos, a fórmula do termo geral é

T k + 1 = - 1 k n k a n - k b k

No nosso caso, n = 5 ,   a = 2 x   e   b = y e 0 ≤ k ≤ n . Então vamos calcular termo a termo (lembrando que temos 6 ):

k = 0 → T 1 = - 1 0 5 0 ( 2 x ) 5 - 0 y 0

k = 1 → T 2 = - 1 1 5 1 2 x 5 - 1 y 1

k = 2 → T 3 = - 1 2 5 2 2 x 5 - 2 y 2

k = 3 → T 4 = - 1 3 5 3 2 x 5 - 3 y 3

k = 4 → T 5 = - 1 4 5 4 2 x 5 - 4 y 4

k = 5 → T 6 = - 1 5 5 5 ( 2 x ) 5 - 5 y 5

Então, temos os seguintes termos:

T 1 = 5 0 32 x 5

T 2 = - 5 1 16 x 4 y

T 3 = 5 0 8 x 3 y 2

T 4 = - 5 0 4 x 2 y 3

T 5 = 5 0 2 x y 4

T 6 = - 5 0 y 5

Passo 11

Agora vamos resolver os números binomiais:

n k = n ! k ! n - k !

Começando:

5 0 = 5 ! 0 ! 5 - 0 ! = 5 ! 5 ! = 1

Lembrando que 0 ! = 1 .

5 1 = 5 ! 1 ! 5 - 1 ! = 5 ! 4 ! = 5

5 2 = 5 ! 2 ! 5 - 2 ! = 5 ! 2 ! 3 ! = 5.4 2 ! = 10

5 3 = 5 ! 3 ! 5 - 3 ! = 5.4 2 ! = 10

5 4 = 5 ! 4 ! 5 - 4 ! = 5 ! 4 ! = 5

5 5 = 5 ! 5 ! 5 - 5 ! = 5 ! 5 ! = 1

Passo 12

Pronto! Agora substituímos:

T 1 = 32 x 5

T 2 = - 5.16 x 4 y

T 3 = 10.8 x 3 y 2

T 4 = - 10.4 x 2 y 3

T 5 = 5.2 x y 4

T 6 = - y 5

Finalmente:

T 1 = 32 x 5

T 2 = - 80 x 4 y

T 3 = 80 x 3 y 2

T 4 = - 40 x 2 y 3

T 5 = 10 x y 4

T 6 = - y 5

Finalizando:

32 x 5 - 80 x 4 y + 80 x 3 y 2 - 40 x 2 y 3 + 10 x y 4 - y 5

Resposta

a   x 4 + 12 x 3 + 54 x 2 + 108 x + 81

b   32 x 5 - 80 x 4 y + 80 x 3 y 2 - 40 x 2 y 3 + 10 x y 4 - y 5