Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo do Centro de Gravidade

Ver Teoria
Exercício 123

Enunciado

Como a constante g é praticamente a mesma em todos os pontos da grande maioria das estruturas, em geral supomos que o centro de gravidade de uma estrutura coincide com o centro de massa. Neste exemplo fictício, porém, a variação da constante g é significativa. A figura abaixo mostra um arranjo de seis partículas, todas de massa m , presas na borda de uma estrutura de massa desprezível. A distância entre partículas vizinhas é 2,00 m

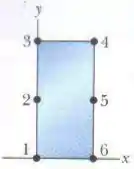
A tabela a seguir mostra o valor de g (em m/s²) na posição de cada partícula. Usando o sistema de coordenadas mostrado na figura, determine:

  1. A coordenada X c m do centro de massa do sistema de seis partículas.
  2. A coordenada Y c m do centro de massa do sistema de seis partículas.

    3. Em seguida, determine:

  3. A coordenada X c g do centro de gravidade do sistema de seis partículas.
  4. A coordenada Y c g do centro de gravidade do sistema de seis partículas.

Passo 1

  1. Aplicando a fórmula de centro de massa, temos:

R → c m = ∑ i ( r → i m i ) ∑ i m i

Para x temos:

X c m = [ 0 + 0 + 0 + m 2,00 + m 2,00 + m 2,00 ] 6 m

X c m = 1,00 m

Passo 2

Para y aplicamos a mesma fórmula:

R → c m = ∑ i ( r → i m i ) ∑ i m i

E, assim, chegamos a:

Y c m = [ 0 + m 2,00 + m 4,00 + m 4,00 + m 2,00 + 0 ] 6 m

Y c m = 2,00 m

Passo 3

Aplicando a fórmula de centro de gravidade, percebemos que como a gravidade não é constante, ela não vai coincidir com o centro de massa.

R → c g = ∑ i ( r → i m i g i ) ∑ i m i g i

Aplicando a fórmula para x:

X c g = 0 + 0 + 0 + m 2,00 7,80 + m 2,00 7,60 + m 2,00 7,40 8,00 m + 7,80 m + 7,60 m + 7,40 m + 7,60 m + 7,80 m

X c g = 0,987 m

Passo 4

Aplicando a fórmula para y:

Y c g = 0 + m 2,00 7,80 + m 4,00 7,60 + m 4,00 7,40 + m 2,00 7,60 + 0 8,00 m + 7,80 m + 7,60 m + 7,40 m + 7,60 m + 7,80 m

Y c g = 1,97 m

Resposta

a)1,00m

b)2,00m

c)0,987m

d)1,97m

Exercícios de Livros Relacionados

Júlia foi contratada para ajudar a pintar a fachada de um prédio, mas não está convencida da segurança do equipamento. Uma prancha de 5,0 m é suspensa horizontalmente, do topo do prédio, por cordas pr
A torre de pisa tem 59,1m de altura e 7,44m de diâmetro. O alto da torre está deslocado 4,04m em relação à vertical. Modele a torre como um cilindro circular homogêneo. (a) Que deslocamento adicional
Uma barra de 10,0m , com 300k g de massa, está colocada sobre uma base, como na Figura 12-32. A barra não está presa, mas simplesmente apoiada sobre uma superfície. Um estudante de 60,0k g tenciona po
Como a constante g é praticamente a mesma em todos os pontos da maioria das estruturas, em geral supomos que o centro de gravidade de uma estrutura coincide com o centro de massa. Neste exemplo fictíc
Como a constante g é praticamente a mesma em todos os pontos da maioria das estruturas, em geral supomos que o centro de gravidade de uma estrutura coincide com o centro de massa. Neste exemplo fictíc