Método de Francis
Produzido por Bruno PestanaTeoria
Faaaaaala meu jovem, tudo certinho?
Nós vimos até agora alguns métodos que servem para resolver sistemas lineares matriciais, até aí tudo ok né?
Mas existe um método que não é muito convencional...

Então, são poucas as universidades que abordam o tema. Se você não vê esse conteúdo, pode pular pro próximo!!!
Basicamente, o Método de Francis ou também conhecido como método QR determina todos os autovalores de uma matriz, sem determinar o polinômio característico (já vimos alguma coisa parecida antes né? É que na real é tudo meio parecido).
Mas, bora lá!
Temos uma matriz quadrada e de ordem , a clássica né! O nosso método vai construir uma sequência de matrizes , ... da seguinte forma: vamos decompondo no produto onde será ortogonal e será a matriz triangular superior.
Então:
O próximo passo é multiplicarmos as duas matrizes na ordem inversa pra formamos a matriz :
Após isso, fazemos a decomposição da matriz:
As matrizes são conjugadas e tem os mesmos autovalores, tudo em ordem aí?
Podemos definir a sequência de matrizes por :
Em que:
O processo só acaba quando termina HAHAHAHHAHAH

Vai acabar quando o maior valor absoluto da matriz (abaixo da diagonal principal) for menor que a precisão dada (ε).
Enquanto não atingimos a precisão necessária nós vamos tentando e encontrando novos e
E como é que eu faço isso?
Como encontramos Q e R?
Queremos
E para isso precisamos achar uma matriz e ortogonal, de modo que quando multiplicamos por zera o elemento .
Vamos achar uma matriz , também ortogonal, para que a multiplicação de por zere agora o elemento . Hmmmm beleza... vamos continuar nessa lógica!
Logo:
E todos esses valores juntos formam .
A partir de agora, vamos usar uma parada chamada matriz rotacional!
Essa matriz é diferente da matriz identidade em 4 sentidos 😊
Agora para outros termos:
Nesse caso para qualquer .
Exemplo:
Exemplo de uma matriz 3 x 3! Para zerar fazemos :
Quando queremos zerar os elementos :
Para zerar os elementos :
Fazemos algo assim:
Assim, temos:
MAAAAAAAAAAAAAAAAAARCA BEM ESSAS DUAS EQUAÇÕES !!!!!!!!!!!!

Primeiro Quando queremos, por exemplo, zerar o termo :
A matriz das “letrinhas” e:
Matricialmente temos:
Segundo zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Terceiro zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Agora, podemos obter e
Então:
E o próximo será:
Fazemos esse passo a passo até que os números abaixo da diagonal principal sejam menores que o erro!
Tudo ok por aqui???
Então, bora fazer exercício para fixar bem esse conteúdo 😊.
Como encontramos Q e R?
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado de Burden, Richard L. Burden | J. Douglas Faires | Annette M. Análise Numérica - Tradução da 10ª edição norte-americana.
Sabe-se da importância da implementação de métodos numéricos, e por isso é muito importante definir-mos quais pontos são necessários para o funcionamento e implementação o que eu desejo obter. Portanto, defina as entradas e saídas para implementar um algoritmo sobre o método de Francis.
Passo 1
Entradas: n; o tamanho da matriz (A) e os termos que a compõem (a) e o número máximo de iterações (M).
Passo 2
Saídas: Valores característicos de A, uma divisão reconhecida de A e a mensagem que excedeu o número de iterações (tol).
Resposta
E: n, A, a, M.
S: A, tol.
Exercício Resolvido #2
Adaptado de Apostila da USP-ICMC de Cálculo numérico (Professora Neide Maria)
Mostre que uma matriz e sua transposta possuem o mesmo polinômio característico:
Passo 1
A equação para encontrar o polinômio característico é:
Sabendo que:
Para ter o mesmo polinômio característico, a matriz A e a transposta devem ser simétricos!
Passo 2
Se as matrizes são simétricas, possuem o mesmo polinômio característico!
Resposta
Simétricas e igual polinômio característico.
Exercício Resolvido #3
Autoria do Responde Aí
Calcule os termos e das seguintes matrizes:
(a)
(b)
Passo 1
(a)
Passo 2
(b)
Resposta
Exercício Resolvido #4
Adaptado de Apostila da USP-ICMC de Cálculo numérico (Professora Neide Maria)
Determinar a primeira iteração para encontrar os autovalores da matriz com o método de Francis:
Com
Passo 1
Se:
Como , devemos zerar apenas o elemento . Assim para obtermos :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 2
Se:
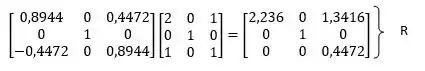
Agora temos que e então , e, portanto .
Com isso:
O termo da matriz triangular inferior
Isso significa que devemos fazer outra iteração.
Resposta
Exercício Resolvido #5
Adaptado de Apostila da USP-ICMC de Cálculo numérico (Professora Neide Maria)
Continue a iteração do exercício anterior:
Com
Passo 1
Se:
Como , devemos zerar apenas o elemento . Assim para obtermos :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 2
Se:
R
Agora temos que e então e
O termo da matriz triangular inferior
Então, os autovalores são os elementos da diagonal principal:
Resposta
Exercício Resolvido #6
Elaboração Própria
Usando o método de Francis na matriz:
É possível estimar seus autovalores aplicando o método uma única vez?
Passo 1
Se:
Não precisamos zerar nem o nem o , pois eles já são . Logo, . Devemos zerar apenas o elemento . Assim :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 2
Se:
R
E então e, portanto:
Com isso:
Opa, como podemos ver, o erro (valor absoluto abaixo da diagonal principal) desse método após uma iteração NÃO deu zero! Logo, NÃO achamos o valor dos autovalores de primeira!!
Resposta
Não
Exercício Resolvido #7
Adaptado de Apostila da USP-ICMC de Cálculo numérico (Professora Neide Maria)
Determinar a primeira iteração para encontrar os autovalores da matriz com o método de Francis:
Passo 1
Se:
Como , devemos zerar apenas o elemento . Assim para obtermos :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 2
Se:
Agora temos que zerar :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 3
Se:
R
E então , e, portanto:
Com isso:
Resposta
Exercício Resolvido #8
Elaboração Própria
Usando o método de Francis uma única vez na matriz:
Encontre o valor de R.
Passo 1
Se:
Devemos zerar o elemento . Assim :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 2
Se:
Agora temos que zerar e, então :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 3
Se:
Agora temos que zerar e, então :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 4
Se:
R
Resposta
Exercício Resolvido #9
Adaptado de Apostila da USP-ICMC de Cálculo numérico (Professora Neide Maria) (ADAPTADO)
Usando o método de Francis uma única vez na matriz:
É possível estimar seus autovalores?
Passo 1
Se:
Não precisamos zerar nem o nem o , pois eles já são . Logo, . Devemos zerar apenas o elemento . Assim :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 2
Se:
R
E então e, portanto:
Com isso:
Opa, como podemos ver, o erro (valor absoluto abaixo da diagonal principal) desse método após uma iteração NÃO deu zero! Logo, NÃO achamos o valor dos autovalores de primeira!!
Resposta
Não.
Exercício Resolvido #10
Elaboração Própria
Usando o método de Francis uma única vez na matriz:
Encontre o valor de R.
Passo 1
Se:
Não precisamos zerar nem o nem o , pois eles já são . Logo, . Devemos zerar apenas o elemento . Assim :
Zeramos o termo :
Onde:
A matriz das “letrinhas” e:
Passo 2
Se:
R