O método das potências
Produzido por Bruno PestanaTeoria
Nós revimos até agora, alguns métodos importantes para encontrar autovalores e autovetores de uma matriz. Mas, vimos também que demanda um tempo maior pra resolver tudo!
Mas relaxa, existem métodos (talvez nem tão triviais assim) que vão permitir encontrar autovalor em módulo e um autovalor associado, de uma matriz A, SEM PRECISAR DESCOBRIR O POLINÔMIO CARACTERÍSTICO!

Um curiosidade sobre essse método, é que ele é responsável pelo ranqueamento de páginas usadas pelo Google.
Maaaaaaaaaaaaaaaaaaaaas, o método serve pra determinar autovalores de módulos grandes ou separados dos demais. É um método da potência é uma técnica iterativa (sim, meus caros... novamente iterações), usada para determinar o autovalor dominante de uma matriz, que basicamente é um autovalor com maior módulo.
Mas a diferença desse método é que ele não encontra SÓ o autovalor, maaaaas, encontra também o autovetor associado.
“O método das potências deriva do fato que as iterações exageram o tamanho relativo dos módulos autovalores”.
Para que o método das potências encontre uma aproximação para o maior autovalor em móduelo de uma matriz , podemos supor também que a matriz tem autovalores e um conjunto de autovetores associados e linearmente independente, devemos supor também que A só tenha valor maior em módulo:
Vamos definir alguns termos:
Desse modo, :
Então:
Agora defina:
De modo análogo, defina a sequiencia de vetores e e uma sequencia de escalares da seguinte forma:
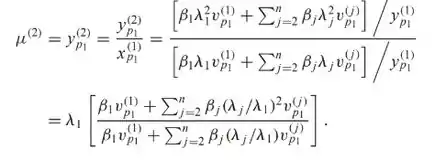
Então vamos para um exemplo para ficar mais claro!
Exemplo
Temos uma matriz A (2 X 2):
Para isso, o exercício dá um vetor inicial :
Então, fazemos o processo de normalização:
Agora, multiplicamos a matriz A pela matriz de vetors normalizados:
O teste de convergência :
Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado de Burden, RLB | .JDF | .AM Análise Numérica - Tradução da 10ª edição norte-americana
Nós vimos outros métodos de encontrar autovalores e autovetores, mas, que esses métodos demandam um tempo computacional além do necessário em alguns casos. Rascunhe quais sãos as entradas e saídas necessárias para implementar o algorítimo para o método das potências.
Passo 1
A primeira coisa que devemos ter em mente é que para obter uma aproximação o para o autovalor dominante e autovetor associado da matriz , de um determinado vetor não nulo x.
Passo 2
Como ENTRADA:
Devemos primeiramente colocar ou pedir para que o usuário determine as dimensões da minha matriz .
Outro valor importante, é pedir os valores que irão compor a matriz .
Além disso, devemos pedir o vetor a tolerância (TOL) e o número máximo de iterações que queremos atingir.
Passo 3
Para Saída: Colocaremos o autovalor aproximado µ, o autovetor aproximado ou uma mensagem dizendo que o número máximo de iterações foi excedido.
Resposta
ENTRADA: , , , TOL, N.
SAÍDA: µ, , N excedido.
Exercício Resolvido #2
Adaptado de Burden, RLB | .JDF | .AM Análise Numérica - Tradução da 10ª edição norte-americana
Verdadeiro e falso:
Marque verdadeiro e falso, e corrija se necessário. Considere como uma matriz diagonalizável com um autovalor dominante .
- Seja for um vetor inicial o maior componente deve ser 1.
- Para a maioria das escolhas de , converge para o autovalor dominante e não converge para um autovalor dominante.
- O nome do Método da Potência deriva do fato de que as iterações exageram o tamanho relativo dos módulos dos autovalores.
Passo 1
- Seja for um vetor inicial o maior componente deve ser 1.
- Para a maioria das escolhas de , converge para o autovalor dominante e não converge para um autovalor dominante.
- O nome do Método da Potência deriva do fato de que as iterações exageram o tamanho relativo dos módulos dos autovalores.
Essa premissa é verdadeira, o vetor inicial é sempre normalizado e transformado em valores vetor
Passo 2
Essa premissa é falsa.
O método da potência é uma técnica iterativa, usada para determinar o autovalor DOMINANTE de uma matriz, e converge para um autovalor dominante.
Passo 2
Verdadeiro.
Resposta
- V
- F
- V
Exercício Resolvido #3
Adaptado de Burden, RLB | .JDF | .AM Análise Numérica - Tradução da 10ª edição norte-americana
Resolva a primeira iteração da matriz abaixo, pelo método das potências, considerando o vetor inicial:
Passo 1
Primeiro passo é fazer:
Se:
Então:
Passo 2
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior 10, que servirá para normalizar:
O vetor , passa a ser
Resposta
Exercício Resolvido #4
Adaptado de documento da Faculdade de Engenharia Resende (Dom Bosco)
Resolva a segunda iteração da matriz abaixo, pelo método das potências, considerando o vetor inicial:
Passo 1
Primeira iteração:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior 7, que servirá para normalizar:
O vetor , passa a ser
Passo 2
Segunda iteração:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser
Resposta
Após 2 iterações:
Exercício Resolvido #5
Adaptado de documento da Faculdade de Engenharia Resende (Dom Bosco)
Resolva a segunda iteração da matriz abaixo, pelo método das potências, considerando o vetor inicial e calcule o erro:
Passo 1
Primeira iteração:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser
Passo 2
Segunda iteração:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser
O erro será:
Resposta
Exercício Resolvido #6
Adaptado de documento da Faculdade de Engenharia Resende (Dom Bosco)
Resolva a primeira iteração da matriz abaixo, pelo método das potências, considerando o vetor inicial e erro :
Passo 1
Primeira iteração:
Se:
Devemos normalizar o vetor:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior 2,8889, que servirá para normalizar:
O vetor , passa a ser
E agora, calculamos o erro:
Passo 2
Segunda iteração:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior 2,9615 , que servirá para normalizar:
O vetor , passa a ser
E agora, calculamos o erro:
Resposta
Após 2 iterações:
Exercício Resolvido #7
Elaboração Própria
Ache o autovetor e o autovalor da matriz abaixo, pelo método das potências, considerando o vetor inicial e erro :
Passo 1
Primeira iteração:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior 7, que servirá para normalizar:
O vetor , passa a ser
E agora, calculamos o erro:
Passo 2
Segunda iteração:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser
E agora, calculamos o erro:
Passo 3
Segunda iteração:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser
E agora, calculamos o erro:
Resposta
Após 3 iterações:
Exercício Resolvido #8
Elaboração Própria
Resolva até a segunda iteração da matriz abaixo, pelo método das potências, considerando o vetor inicial e encontre o erro na ultima iteração:
Passo 1
Primeira iteração) Primeiro passo é fazer:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser
Passo 2
Primeiro passo é fazer:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser:
O erro será:
Resposta
Exercício Resolvido #9
Apostila algorítimos numéricos da Universidade Federal do Espírito Santo
Resolva até a segunda iteração da matriz abaixo, pelo método das potências, considerando o vetor inicial e encontre o erro na ultima iteração :
Passo 1
Primeira iteração) Primeiro passo é fazer:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior 1231,8 , que servirá para normalizar:
O vetor , passa a ser
Passo 2
Primeiro passo é fazer:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser:
Resposta
Exercício Resolvido #10
Elaboração Própria
Resolva até a segunda iteração da matriz abaixo, pelo método das potências, considerando o vetor inicial e encontre o erro na ultima iteração:
Passo 1
Primeira iteração) Primeiro passo é fazer:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior 6 , que servirá para normalizar:
O vetor , passa a ser
Passo 2
Primeiro passo é fazer:
Se:
Então:
No próximo passo, devemos transformar a matriz calculada em uma matriz normalizada .
Onde µ será o termo maior , que servirá para normalizar:
O vetor , passa a ser:
O erro será: